树状数组

一、树状数组长什么样子？

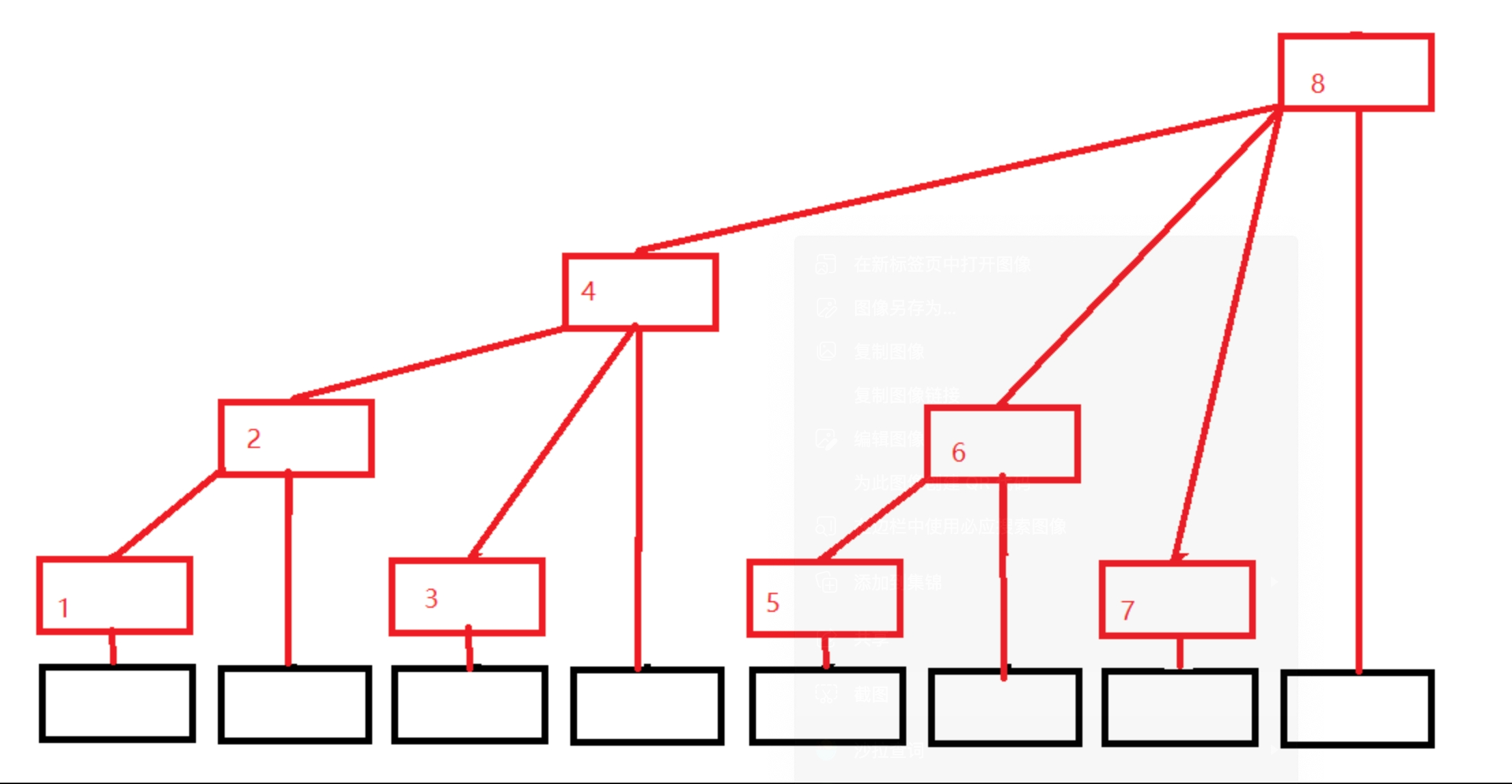
黑色数组代表原来的数组（下面用A[i]代替），红色结构代表我们的树状数组(下面用C[i]代替)，发现没有，每个位置只有一个方框，令每个位置存的就是子节点的值的和，则有

• C[1] = A[1];
• C[2] = A[1] + A[2];
• C[3] = A[3];
• C[4] = A[1] + A[2] + A[3] + A[4];
• C[5] = A[5];
• C[6] = A[5] + A[6];
• C[7] = A[7];
• C[8] = A[1] + A[2] + A[3] + A[4] + A[5] + A[6] + A[7] + A[8];

二、有什么的规律呢？

这颗树是有规律的，其中

$C[i] = A[i-2^k+1] + A[i - 2^k+2] + ... + A[i];$ //k为i的二进制中从最低位到高位连续零的长度

例如i = 8(1000)时候，k = 3，可自行验证。

这个怎么实现求和呢，比如我们要找前7项和，那么应该是$SUM = C[7] + C[6] + C[4];$

而根据上面的式子，容易的出$SUM(i) = C[i] + C[i-2^{k1}] + C[(i - 2^{k1}) - 2^{k2}] + .....；$

其实树状数组就是一个二进制上面的应用。

现在新的问题来了$2^k$该怎么求呢，不难得出$2^k$ = i&(i^(i-1));但这个还是不好求出呀，前辈的智慧就出来了，$2^k$= i&(-i);

三、何为lowbit？

i & (-i)我们称之为lowbit，它的结果就是$2^k$。

证明：

这里利用的负数的存储特性，负数是以补码存储的，对于整数运算 x&(-x)有

• 当x为0时，即 0 & 0，结果为0；
• 当x为奇数时，最后一个比特位为1，取反加1没有进位，故x和-x除最后一位外前面的位正好相反，按位与结果为0。结果为1。
• 当x为偶数，且为2的m次方时，x的二进制表示中只有一位是1（从右往左的第m+1位），其右边有m位0，故x取反加1后，从右到左第有m个0，第m+1位及其左边全是1。这样，x& (-x) 得到的就是x。
• 当x为偶数，却不为2的m次方的形式时，可以写作$x= y * (2^k)$。其中，y的最低位为1。实际上就是把x用一个奇数左移k位来表示。这时，x的二进制表示最右边有k个0，从右往左第k+1位为1。当对x取反时，最右边的k位0变成1，第k+1位变为0；再加1，最右边的k位就又变成了0，第k+1位因为进位的关系变成了1。左边的位因为没有进位，正好和x原来对应的位上的值相反。二者按位与，得到：第k+1位上为1，左边右边都为0。结果为$2^k$。

总结一下：x&(-x)，当x为0时结果为0；x为奇数时，结果为1；x为偶数时，结果为x中2的最大次方的因子。

代码实现：

int lowbit(int x)
{
    return x & (-x);
}

四、如何求和

$SUM(i) = C[i] + C[i-2^{k1}] + C[(i - 2^{k1}) - 2^{k2}] + ...$

代码实现：

int a[MAXN], c[MAXN]; // MAXN是最大的个数
int lowbit(int x)
{
    return x & (-x);
}
int getSum(int i) // i为第i个数， 求得的结果是从1到i位置数的和
{
    int ret = 0;
    while(i > 0)
    {
        ret += c[i];
        i -= lowbit(i);
    }
    return ret;
}

五、如何单点更新值

因为$C[i] = A[i-2^k+1] + A[i - 2^k+2] + ... + A[i]$，那么如果我们更新某个A[i]的值，则会影响到所有包含有A[i]位置。如果求A[i]包含哪些位置里呢，同理有

$A[i]$包含于 $C[i + 2^k]、C[(i + 2^k) + 2^k]...$

代码实现：

void update(int i, int k) // i位置上加上k
{
    while(i <= n)
    {
        c[i] += k;
        i += lowbit(i);
    }
}

建树的时候，直接用update即可，相当于在原来的位置上加上值。

这样我们就实现了单点修改，区间查询。

六、单点修改、区间查询的模板

const int N = 1e5 + 5;
int n;
int a[N], c[N];
int lowbit(int x) { return x & (-x); }
void update(int i, int k)
{
    while (i <= n)
    {
        c[i] += k;
        i += lowbit(i);
    }
}
int getSum(int i)
{
    int res = 0;
    while(i > 0)
    {
        res += c[i];
        i -= lowbit(i);
    }
    return res;
}
int main(void)
{
    cin >> n;
    for (int i = 1; i <= n; ++i)
    {
        cin >> a[i];
        update(i, a[i]);
    }
    int q;
    for (int i = 1, left, right; i <= q; ++i)
    {
        cin >> left >> right;
        cout << getSum(right) - getSum(left - 1) << endl;
    }
}

如果我们要实现区间修改，单点查询怎么办？

七、区间修改、单点查询怎么办？

在某一区间$[left, right]$每一个数都加上k，这个可以用差分数组来实现，单点查询修改前的值直接用a数组$O(1)$复杂度实现，单点查询修改后的值就可以用树状数组存差分即可。

差分的知识在不此详述。

单点查询就是差分的和。

[浴谷p3374]:https://www.luogu.com.cn/problem/P3374 为例

实现代码：

#include <iostream>
using namespace std;

const int N = 5E5 + 5;
int n, m;
int a[N], c[N], d[N];
int lowbit(int x) { return x & (-x); }
void update(int i, int k)
{
    while (i <= n)
    {
        c[i] += k;
        i += lowbit(i);
    }
}
int getSum(int i)
{
    int res = 0;
    while (i > 0)
    {
        res += c[i];
        i -= lowbit(i);
    }
    return res;
}
int main(void)
{
    ios::sync_with_stdio(0);
    cin.tie(0);

    cin >> n >> m;
    for (int i = 1; i <= n; ++i)
    {
        cin >> a[i];
        d[i] = a[i] - a[i - 1];
        update(i, d[i]);
    }
    int x, y, t, k;
    for (int i = 0; i < m; ++i)
    {
        cin >> t;
        if (t == 1)
        {
            cin >> x >> y >> k;
            update(x, k);
            update(y + 1, -k);
        }
        if (t == 2)
        {
            cin >> x;
            cout << getSum(x) << endl;
        }
    }
    return 0;
}

八、区间修改、区间查询怎么办？

上面我们说的差值建树状数组，得到的是某个点的值，那如果我既要区间更新，又要区间查询怎么办。这里我们还是利用差分，由上面可知

$ \sum\limits_{i = 1}^n A[i] = \sum\limits^n_{i = 1} \sum\limits^i_{j = 1}D[j];$

则

$A[1]+A[2]+...+A[n]$

$= (D[1]) + (D[1]+D[2]) + ... + (D[1]+D[2]+...+D[n]) $

$= n\times D[1] + (n-1)\times D[2] +... +D[n]$

$= n \times (D[1]+D[2]+...+D[n]) - (0\times D[1]+1\times D[2]+...+(n-1)\times D[n])$

所以上式可以变为$\sum\limits^n_{i = 1}A[i] = n\times \sum\limits^n_{i = 1} D[i] - \sum\limits^n_{i = 1}( D[i]*(i-1) );$

这里我们维护两个数状数组，sum1[i] = D[i]，sum2[i] = D[i]*(i-1);即可

int n,m;
int a[50005] = {0};
int sum1[50005];    //(D[1] + D[2] + ... + D[n])
int sum2[50005];    //(1*D[1] + 2*D[2] + ... + n*D[n])

int lowbit(int x){
    return x&(-x);
}

void updata(int i,int k){
    int x = i;    //因为x不变，所以得先保存i值
    while(i <= n){
        sum1[i] += k;
        sum2[i] += k * (x-1);
        i += lowbit(i);
    }
}

int getsum(int i){        //求前缀和
    int res = 0, x = i;
    while(i > 0){
        res += x * sum1[i] - sum2[i];
        i -= lowbit(i);
    }
    return res;
}

int main(){
    cin>>n;
    for(int i = 1; i <= n; i++){
        cin>>a[i];
        updata(i,a[i] - a[i-1]);   //输入初值的时候，也相当于更新了值
    }

    //[x,y]区间内加上k
    updata(x,k);    //A[x] - A[x-1]增加k
    updata(y+1,-k);        //A[y+1] - A[y]减少k

    //求[x,y]区间和
    int sum = getsum(y) - getsum(x-1);

    return 0;
}