chjshen 的博客
C++语法基础3-循环结构
chjshen 教练 LV 5 SU @ 2023-11-21 9:03:37

循环结构

一、while语句

“长亭外，古道边...” -- 《送别》

国学大师告诉大家，当我们还不会背书的时候，就一直读啊，读啊，读啊，读着读着就会背了。

1、背书循环

while(不会背)
{
   背书;
}
看电视

循环轮次	会背了吗？	背书
1	不会(一开始)	长亭外，古道边...
2	不会	长亭外，古道边...
3		长亭外，古道边....
4		长亭外，古道边...
...	......
n	会了	退出背书的循环，看电视去

2、while语句要素

初始状态;
  while(表达式) 
  {
    语句; 
    状态变化;
  }
  后续语句;

例如：大师告诉小明，背书10遍就可以看电视了。

int i = 0;
  while (i < 10)
  {
    cout << "长亭外，古道边" << endl;
    i++;
  }
  cout << "终于可以看电视了" << endl;

3、要素的理解

退出条件：背10遍，那么i == 10就退出（从0开始）
循环条件：i < 10

进入：i = 0时，表达式为true
循环：i++ 并且小于10时，表达式为true
退出：i ++ 为10时，表达式为false

状态：
- 初始：i = 0
- 变化：i++
- 退出：i == 10
执行语句：用来放置在循环里执行的业务，例如输出啊，运算啊之类。

二、死循环

1、死循环

如果表达式永远是true，则while就会一直在里面循环，这种情况称之为死循环。

2、死循环的形式-主动死循环

主动死循环指特意写成死循环结构，为了某种场景应用。

例如死循环接受键盘输入，输入q退出，其它字符作为指令进行处理。

char c;
  while (true) //死循环
  {
    cout << "输入一个字符，q表示退出：";
    cin >> c;
    if (c == 'q')
      break;
    cout << "你输入的是：" << c << endl;
  }

3、bug死循环

bug死循环指由于代码写的不好，导致循环退不出。

这种情况的危害很大，严重的甚至会导致计算机资源耗光死机，在编写循环结构的时候要特别注意。

例如以下代码：

int i = 1;
  while (i != 10)
  {
     语句;
     i += 2; // i = i + 2;
  }

4、break跳出循环

循环的退出，一种方法是表达式变成false，另一种方法是显示的调用break语句。

当在循环里执行break语句时，立即跳出循环（不会执行break后面的语句）。

while(true)
  {
    语句1;
    break;
    语句2；//这句执行不到了
  }

5、break的if表达式与while表达式的关系

一般循环有两种形态：while(表达式)与while(true)+break：

while(表达式)
```
while(i <= 10)
{
  ......
}
```

while(true) + break

while(true)
{
  .....
  if (i > 10) break;
}

if的表达式，一般为while表达式的取反，（或边界条件）。

三、for语句

在while里，我们学到了循环结构的知识：

表达式：
- 初始值：初始状态使得表达式初始值为真，从而进入循环。
- 中间值：状态变化，表达式的值继续为真，保持循环。
- 结束值：状态变化，表达式值变成假，退出循环。
状态变量：
- 初始值：状态开始的值，使得表达式为真，进入循环。
- 状态变化：在每次循环时变化状态，到某个状态值时，表达式变成假，退出循环。
执行语句
- 语句体，在循环里面执行具体的业务。

在很多案例里，表达式和状态都是类似的，例如：

表达式：i < 1000
状态变化：i++

真正变化的都是执行语句，如在循环里执行输出、累加等等。

for语句结构将初始状态、表达式、状态变化都提炼到了语句结构里，语句体里只保留了执行语句。

for(int i=0; i< 10; i++) //for结构
  cout << i << endl; //执行语句

1、for语句

//for里面的三个部分，中间用分号;隔开
//for(初始状态; 表达式; 状态变化)
for(i=0; i<10; i++)
{
  //执行语句
  cout << i << endl;
}

for语句把控制部分（初始状态、表达式、状态变化）提炼到了一起，使结构更加清晰，但背后逻辑与while结构是一样的：

第一步，设初始状态：i = 0。
第二步，判断表达式，为真进入循环，否则退出：i < 10。
第三步，执行语句（循环体里的语句）：cout << i << endl;
第四步，状态变化：i++
第五步，继续判断表达式，为真继续循环，否则退出： i < 10。

图解：

轮次	状态	表达式结果	执行语句
1	0	true	`cout << 0 << endl;`
2	1		`cout << 1 << endl;`
3	2		cout << 2 << endl;
4	3		cout << 3 << endl;
5	4		cout << 4 << endl;
6	5		cout << 5 << endl;
7	6		cout << 6 << endl;
8	7		cout << 7 << endl;
9	8		cout << 8 << endl;
10	9		cout << 9 << endl;
11	10	false	循环退出

2、for与while

案例：输出1-10的数字。

while结构：

int i = 1;
while(i <= 10)
{
  cout << i << endl;
  i++;
}

for结构：

for(int i=1; i<= 10; i++)
  cout << i << endl;

3、for循环变体

在for结构里，也可以把某个控制部分迁移到循环里面去，效果与原来类似，例如：

初始状态迁移

int i = 0;
//保留一个分号
for(; i <= 10; i++)
  .....

表达式迁移

//表达式迁移了，分号还在
for(int i = 0;  ; i++)
{
  cout << ....;
  //表达式放这里，注意退出条件和循环条件相反
  if (i > 10) break;
}

状态变化迁移：

for(int i = 0; i <= 10; )
{
   cout << ....;
   i++;  //状态变化放这里了
}

四、for 与 if 结合

小明刚学习了for循环的知识，他很熟练的输出了0-10的数字，现在老师让他只输出0-10里面的偶数。

1、for循环的理解

for循环的循环体传入一个状态变量的多个值，例如1， 2， 3， 4....，如果执行语句是输出就直接把每个状态变量都输出了。

2、if 语句判断偶数

对于循环体传进来的每个状态变量，可以用if语句，使用关系表达式 i % 2 == 0判断是否是偶数，当状态变量是偶数时输出，否则跳过（到下一轮循环）。

for(......)
{
    if (关系表达式)
       //执行语句
}

如果if(关系表达式)不满足，则继续执行for的控制语句（i++，然后下一个）。

五、多重循环

小明问老师怎么才能学好编程？老师说：每周从周一到周日都要练习编程，每天编写五份代码，这样学习就会比较有效。

1、循环嵌套

循环体里面可以继续使用循环，一般用的比较多的是二重循环，例如：

while(条件1)
{
  //循环语句1
  while(条件2){
     //循环语句2
  }
}

for(循环条件1)
{
  //循环语句1
  for(循环条件2){
    //循环语句2
  }
}

do{
   //循环语句1
   for(循环条件2){
     //循环语句2
   }
}while(循环条件1);

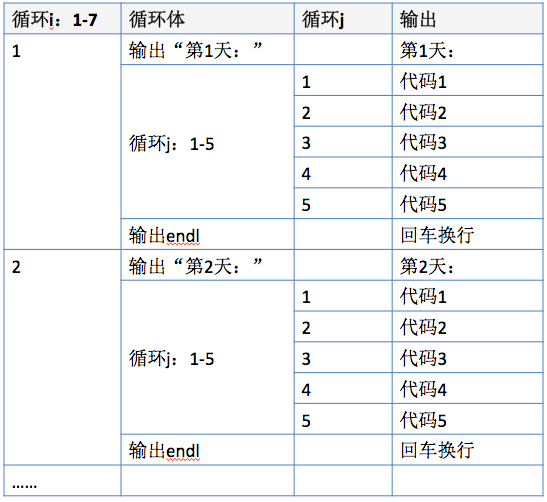
2、例子

for(int i=1; i<=7; i++)
  {
    cout << "第" << i << "天：";
    for(int j=1; j<=5; j++)
      cout << "代码" << j << " ";
    cout << endl;
  }

输出：

第1天：代码1 代码2 代码3 代码4 代码5 
第2天：代码1 代码2 代码3 代码4 代码5 
第3天：代码1 代码2 代码3 代码4 代码5 
第4天：代码1 代码2 代码3 代码4 代码5 
第5天：代码1 代码2 代码3 代码4 代码5 
第6天：代码1 代码2 代码3 代码4 代码5 
第7天：代码1 代码2 代码3 代码4 代码5

第一行表示i=1时运行j=1..5。

3、循环次数

外层循环的下标从1-7，共循环7次。
内层循环的下标从1-5，每次外循环，内循环都要5次。
总共循环次数是7*5 ＝ 35 次。

多重循环次数

4、扩展理解

问题：如果三重循环i从1到10、j从1到20、k从1到5，总共循环次数是多少？

答案：10 * 20 * 5 = 500 次

WA  == wrong answer
TLE == Time limit error
AC  == answer correct
CE  == compile error

5、同余定理

模运算与基本四则运算有些相似，但是除法例外。其规则如下：

(a + b) % p = (a % p + b % p) % p

（1） (a - b) % p = (a % p - b % p) % p

（2） (a * b) % p = (a % p * b % p) % p

（3） a ^ b % p = ((a % p)^b) % p

（4）结合律： ((a+b) % p + c) % p = (a + (b+c) % p) % p

（5） ((ab) % p * c)% p = (a * (bc) % p) % p

（6）交换律： (a + b) % p = (b+a) % p

（7） (a * b) % p = (b * a) % p

（8）分配律： ((a +b)% p * c) % p = ((a * c) % p + (b * c) % p) % p

重要定理

若a≡b (% p)，则对于任意的c，都有(a + c) ≡ (b + c) (%p)；

（10）若a≡b (% p)，则对于任意的c，都有(a * c) ≡ (b * c) (%p)；

（11）若a≡b (% p)，c≡d (% p)，

则 (a + c) ≡ (b + d) (%p)，

(a - c) ≡ (b - d) (%p)，

(a * c) ≡ (b * d) (%p)，

(a / c) ≡ (b / d) (%p)；

C++语法基础3-循环结构