chjshen 的博客
数据结构-图的遍历之DFS
chjshen 教练 LV 5 SU @ 2023-6-1 7:05:04

图的遍历之DFS

1、图的遍历

图的遍历：从图的某个顶点出发，按照某种搜索方法沿着图的边访问所有顶点，每个顶点仅访问一次。

遍历得到的顶点的序列，称为图遍历序列。显然不同的搜索方法会得到不同的遍历序列。

有两种搜索方法：

深度优先搜索（DFS：Depth First Search）
广度优先搜索（BFS：Breadth First Search）

2、深度优先搜索

从某个顶点v0出发，找到其第一个邻接点v1，从v1开始继续进行深度优先搜索，如果某个顶点没有未访问的邻接点，就沿着原路回溯，一直到所有的顶点都被遍历到（既回溯到开始搜索的地方）。

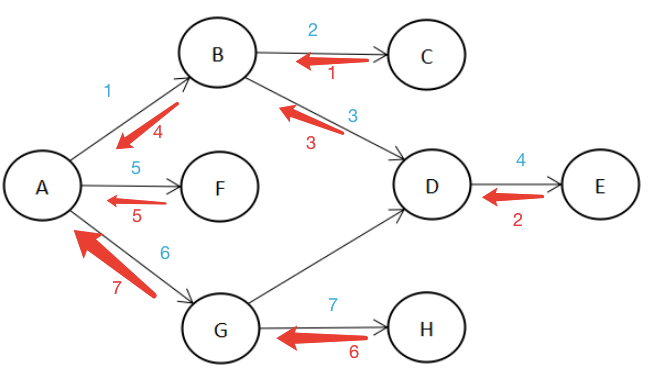
上图从A点出发做dfs搜索（蓝字表示访问，红字表示回溯）：

访问A点，邻接点有B、F、G，选择B点
访问B点，邻接点有C、D，选择C点
访问C点，没有邻接点，返回
回溯到B点，未访问点有D，选择D点
访问D点，邻接点有E，选择E点
访问E点，没有邻接点，返回
回溯到D点，没有未访问点，返回
回溯到B点，没有未访问点，返回
回溯到A点，未访问点有F、G，选择F
访问F点，没有邻接点，返回
回溯到A点，未访问点有G，选择G
访问G点，未访问点有H，选择H
访问H点，没有邻接点，返回
回溯到G点，没有未访问点，返回
回溯到A点，没有未访问点，返回
回到搜索调用的地方，搜索结束

遍历序列为：ABCDEFGH

理解dfs：尽可能的远离起始点。

3、算法实现

要点描述：

根据邻接矩阵（或邻接表）能遍历每个点的邻接点
已经访问的点，用一个桶数组vis[]记录，防止重复经过
用递归函数实现往下遍历
也可以用栈(stack)来实现

dfs(顶点) {
  记录访问;
  for(邻接点)
    if (没有访问过)
      dfs(邻接点);
}

int main(){
  dfs(起始点);
  return 0;
}

如果图不一定连通，调用dfs的时候需要用到循环

int main() {
  for(int i=1; i<=n; i++)
    if(!vis[i])
      dfs(i);
}

注意：

dfs遍历经过所有点和边，其复杂度为O(V+E)
dfs遍历时没有对状态回溯，如果加上状态回溯就变成了枚举所有的路径

扩展理解

dfs使用递归进行遍历，每个顶点都有进入、退出的时机，注意退出时机是和递归调用反着的。

4、dfs回溯

在dfs遍历时，往往通过vis数组标记经过的点（或边），这是为了避免回路，这种情况下往往只有一条路径可走。

如果我们想枚举所有的路径，就要对vis状态进行回溯，例如：

void dfs(int x) {
  vis[x] = true;
  for(int i=0; i<g[x].size(); i++) {
    int y = g[x][i];
    if(!vis[y])
      dfs(y);
  }
  vis[x] = false;  //这句话对vis[x]进行回溯，使得能遍历所有路径
}

5、保存路径

dfs回溯遍历所有路径，可以用数组将路径保存起来，一般数组的元素可为路径上的点（或边）。

例如：

void dfs(int x) {
  vis[x] = true;
  path[++last] = x;   //保存路径的节点
  for(int i=0; i<g[x].size(); i++) {
    int y = g[x][i];
    if(!vis[y])
      dfs(y);
  }
  vis[x] = false; 
  last--;   //回溯，删除路径上的这个点，给后面其它点用
}

保存路径之后，在触发某些条件时，就可以输出/计算路径。

例如－输出所有到达fx的路径：

void dfs(int x) {
  if(x == fx) { //到达fx点时输出路径
    for(int i=1; i<=last; i++)
      cout<<path[i]<<" ";
    cout<<fx<<" "<<endl; //注意此时fx还没有被数组保存，因此..
    return;
  }
  vis[x] = true;
  path[++last] = x;   //保存路径的节点
  for(int i=0; i<g[x].size(); i++) {
    int y = g[x][i];
    if(!vis[y])
      dfs(y);
  }
  vis[x] = false; 
  last--; 
}

注意：dfs遍历的顺序，与图的存储有关，因此多个路径的先后不是唯一的。

6、最长/最短距离

有时候题目不需要输出具体的路径，只需要求出最长/最短距离，就可以在递归回溯的同时直接计算距离，进行最大最小判断。

void dfs(int x, int sum) {
  if(x == fx) { //求到达fx的最长距离
    ans = max(ans, sum);
    return;
  }
  vis[x] = true;
  path[++last] = x;   //保存路径的节点
  for(int i=0; i<g[x].size(); i++) {
    int y = g[x][i].y, w=g[x][i].w;
    if(!vis[y])
      dfs(y, sum+w); //传入距离参数，自动回溯
  }
  vis[x] = false; 
  last--; 
}

原理：在递归函数里传入距离参数，参数是会自动回溯的。

剪枝优化：对正权图求最小距离，可以剪枝优化，即如果当前dfs函数传入的sum>=ans，则再走下去也肯定会比ans大，因此可以直接返回。

void dfs(int x, int sum) {
  if(sum >= ans) return; //剪枝
  if(x == x0) { //求到达x0的最小距离
    ans = min(ans, sum);
    return;
  }
  ......

数据结构-图的遍历之DFS