图

1、什么是图

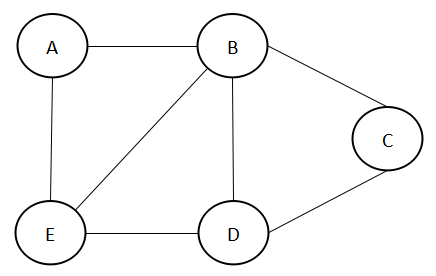
以上就是一个图，包含5个顶点和7条边。简单的说，把点用边连起来，就叫做图。

定义：G = (V, E)

• G（graph）：表示一个图
• V（Vertext）：顶点（结点），非空有限集合
• E（Edge）：边的集合，可以为空

2、图的分类

2.1 无向图

如果图的边没有方向，称之为无向图。上面的例子就是一个无向图。

无向图的边（Edge），用(V1, V2)表示。

2.2 有向图

如果图的边有方向，称之为有向图，如下图：

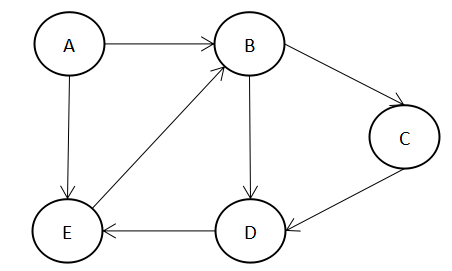
有向图的边用<V1, V2>，表示方向从V1到V2，也称为弧（Arc），V1为弧尾（Tail），V2为弧头（Head）。

2.3 加权图（网图）

如果一个图的边带有一个数值（通俗理解为边的“长度”，只是权可以为负数），就把这样的图称之为“加权图”，边上带有的数值称为“权”。

无向图带有权，称之为“无向加权图”，有向图带有权，称之为“有向加权图”。

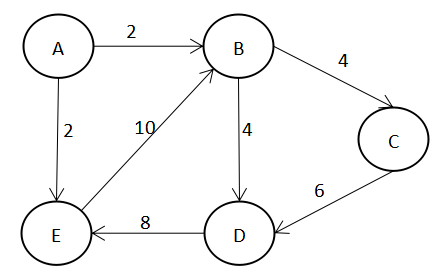
3、邻接矩阵

图的顶点可用一个一维数组来存储，如果只有编号的话一般都默认1到n即可。

图的边一般使用邻接矩阵或邻接表来存储，特殊情况下也可以使用边的数组来存储。

大部分情况下，noi算法题都使用邻接矩阵来表示图，因此我们这里先学习邻接矩阵。

3.1 邻接矩阵

使用二维数组来存储图中所有边，a[x][y]的值表示一条边（x, y）或<x, y>的信息。

例如对于本例的无向图：

其邻接矩阵如下：

0	1	0		1
1	0	1	1	1
0	1	0		0
		1	0	1
1		0	1	0

以上1表示连接，0表示无连接，行列下标分别表示A、B、C、D、E顶点。

对称性：无向图的邻接矩阵是对称的，既a[x][y] = a[y][x]。

3.2 有向图的邻接矩阵

对有向图来说，邻接矩阵也是适用的，只是不对称。

其邻接矩阵如下：

0	1	0		1
0	0	1	1	0
		0
			0	1
	1			0

3.3 加权图的邻接矩阵

对加权图来说，邻接矩阵的值就不能只是1或0了，需要存储边的权。

有向加权图的邻接矩阵如下：

0	2	0		2
0	0	4		0
		0	6
			0	8
	10			0

注意：为了避免有权的值是0，有时候需要将"无连接的边"设计为不会出现的数值，例如无穷大。

4、图的输入

如果用邻接矩阵来表示一个图，就需要将输入的信息转化为邻接矩阵，俗称“建边”。

如果一个试题输入就是一个邻接矩阵，显然就直接读取就好。

有时候，一个试题会输入点和边的数目n、m，然后输入m行，每行用两个点x、y表示边(x, y)。

例如-第一行n和m，接下来m行都是边：

5 5
1 2
2 3
2 4
3 4
4 5

这种情况，就需要根据边(x, y)进行建边：

int n, m, x, y;
cin>>n>>m;
for(int i=1; i<=m; i++)
  cin>>x>>y;
  g[x][y] = g[y][x] = 1; //对称

注意：

• 如果是有向图，则不需要考虑对称。
• 如果是权图，则每行输入三个数，表示权为z的边(x, y) 。

扩展理解

1、图的表示

如何表示一个图？

• 图形
• 点集与边集
• 邻接矩阵
• 邻接表
• 关联矩阵

第一个是肉眼能显然理解的图形，后面都是代码里存储的数据。

我们需要习惯在图形与数据之间切换，做到对着数据能轻松看懂对应图的结构，这样对学习图论就会很有帮助。

上图的输入：

5 7
A B C D E
1 2
1 5
2 3
2 4
3 4
4 5
5 2

邻接矩阵内容：

0	1	0		1
0	0	1	1	0
		0
			0	1
	1			0

邻接表内容：

顶点	边1	边 2	.....
A	2	5
B	3	4
C	4
D	5
E	2

2、邻接矩阵与桶数组

如果学过桶数组，就会比较容易理解邻接矩阵。

第i行是一个数组，表示编号i的顶点，所连接的边，使用了桶数组来存储。

下标i和j表示图中任意两个点，g[i][j]的值用来规定两个点连接的信息，例如：

• true表示连接、false表示不连接
• 数值表示边上的权，inf表示不连接
• ......

5、邻接表

用邻接矩阵来表示图，需要用到二维数组，其中很多没有连接的边也都需要占位，占内存比较大，运算复杂度也高。

另外一种方式就是使用邻接表，只存储每个顶点连接的边（边的个数不定）。这样对于大的稀疏图就可以节约大量的内存，同时访问起来更加快速。

邻接表核心结构：

• 顶点用一维数组存储
• 每个顶点的所有邻接边构成一个长度不定的线性表

由于邻接边的动态特性，一般可使用结构体＋指针（单向链表）的方式来实现邻接表，但如果对链表知识没有掌握的同学，也可以采用其它方法实现动态线性表，例如Vector、链式前向星等。

6、邻接表案例

邻接表内容：

顶点	边1	边 2	.....
A	2	5
B	3	4
C	4
D	5
E	2

7、Vector实现

Vector是c++ stl库提供的可变大小的序列容器，基本操作：

• 头文件：#include
• 声明变量：vector vec
• 增加元素：vec.push_back(a)
• 下标访问：vec[i]，从0开始到vec.size()-1

可变大小的特性用来实现邻接表非常合适:

注：可理解成动态长度的数组。

7.1 邻接表定义

vector<int> g[N];//用vector存储每个顶点连接的边

如果加权图，可用一个结构体，例如：

struct Edge {
  int y; //边连接的顶点
  int w; //权
};
vector<Edge> g[N];

也可用边数组Edge e[M]存储每条边，然后g[x]里存放边的序号（数组下标），例如：

7.2 建边

直接在vector里存边：

cin>>x>>y; //输入一条边
g[x].push_back(y);  //新增一条边
//加权图增加结构体：g[x].push_back((Edge){y, w}); 
//无向图一条边加两次：g[y].push_back(x);

或vector里存边的序号：

cin>>x>>y;
e[i] = (Edge) {x, y}
g[x].push_back(i);

7.3 遍历

for(int j=0; j<g[i].size();  j++)
  访问 g[i][j];

8、指针单链表实现

把同一个顶点连接的所有边以单链表的方式连接起来，访问的时候按照next元素循环读取。

常见的实现是用结构体＋指针实现单链表。

相比较vector的实现，单链表理解起来要晦涩一些，因此我们建议用vector方式更好，当然如果是超大图存在内存与时间要求的，使用单链表会有性能的优势。

8.1 邻接表定义

struct Edge {
  int end;
  Edge *next;
};
Edge* g[N];

8.2 建边

Edge* e = new Edge;
      e->end = y[i];
      e->next = g[x[i]];
      g[x[i]] = e;
    }

以上主要是把新的边作为第一条边，其next指向旧的第一条边。

8.3 遍历

for(Edge* e=g[i]; e!=NULL; e=e->next)
      //访问e

9、链式前向星实现

这是用静态数组实现单链表的一种技巧，将每个边用结构体的形态存储成一个边集（数组），每个边的next指向同一起点的下一条边在边集里的的序号，事实上就是一个链表。

g[N]为邻接表，存储每个顶点连接的第一条边（在边集里的序号）。

9.1 定义

struct Edge {
  int end;//终点
  int next;//下一条边的序号，0表示没有
};
Edge e[M];//边数组，其下标做为边的编号
int g[N];//邻接表，存储第一个edge

9.2 建边

e[i].end = y[i];
    e[i].next = g[x[i]];
    g[x[i]] = i;

9.2 遍历

for(int j=g[i]; j>0; j=e[j].next)
      //访问e[j]

扩展理解

1、结构体

结构体将多个字段聚合成一个类型，用struct关键字定义：

struct Person {
  string name;
  int age;
};

Person p1, p2, p3;

注意：以上是c++语法，在c语言中，变量声明前要加struct。

2、访问成员

结构体变量的成员，通过.来访问，例如：

Person p1;
p1.age = 20;

如果是指针变量，则通过->来访问，例如：

Person *p1 = new Person;
p1->age = 20;

3、指针释放

对于new出来的指针，需要显示调用delete进行释放，否则会内存泄露。

Person *p1 = new Person;
delete p1;

4、反图

有时候，需要存储一个图的反图：

g1[x].push_back(y);//正图
g2[y].push_back(x);//反图