chjshen 的博客
数据结构-特殊树之二叉搜索树BST
chjshen 教练 LV 5 SU @ 2023-5-31 22:22:48

二叉排序树

二叉排序树（Binary Sort Tree，简称 BST ）又叫二叉查找树和二叉搜索树，是一种实现动态查找表的树形存储结构。

二叉排序树本质是一棵二叉树，它的特别之处在于：

对于树中的每个结点，如果它有左子树，那么左子树上所有结点的值都比该结点小；
对于树中的每个结点，如果它有右子树，那么右子树上所有结点的值都比该结点大。
它的左子树和右子树都是二叉排序树

举个简单的例子，下图就是一棵二叉排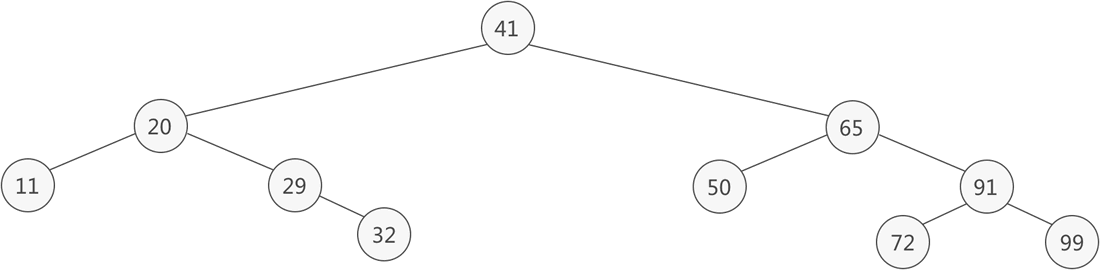序树：图 1 二叉排序树以根节点为例，左子树上所有结点的值都比 41 小，右子树上所有结点的值都比 41 大。不仅是根结点，整棵二叉树上的非叶子结点都是如此，这样的二叉树就是一棵二叉排序树。

二叉排序树的具体应用

二叉排序树的常见操作有 3 种，分别是：

SearchBST(Key)：查找指定的元素 Key；
InsertBST(Key)：若二叉排序树中不存在元素 Key，将 Key 作为新结点插入到树上的适当位置；
DeleteBST(Key)：若二叉排序树中存在元素 Key，将存储 Key 的结点从树中摘除。

接下来一一讲解这 3 种操作的实现思路，并给出可参考的实现代码。

1、二叉排序树查找元素

在二叉排序树中查找目标元素，就是从树根结点出发，先将树根结点和目标元素做比较：

若当前结点不存在，则查找失败；若当前结点的值和目标元素相等，则查找成功；
若当前结点的值比目标元素大，目标元素只可能位于当前结点的左子树中，继续进入左子树查找；
若当前结点的值比目标元素小，目标元素只可能位于当前结点的右子树中，继续进入右子树查找；

以图 1 中的二叉排序树为例，查找元素 32 的过程是：

从树根结点出发，41 比目标元素 32 大，则 32 只可能位于 41 的左子树中，继续进入左子树查找；
当前子树的根结点 20 比目标元素 32 小，则 32 只可能位于 20 的右子树中，继续进入右子树查找；
当前子树的根结点 29 比目标元素 32 小，则 32 只可能位于 29 的右子树中，继续进入右子树查找；
当前子树只有一个根结点 32，和目标元素相等，正是要找的目标元素。

整个查找过程如下图所示：图 2 查找目标元素 32 的过程

编码实现在二叉排序树中查找目标元素，可以参考如下的程序：

BiTree SearchBST(BiTree T, KeyType key) {
    //如果 T 为空，则查找失败，返回NULL；或者查找成功，返回指向存有目标元素结点的指针
    if (!T || key == T->data) {
        return T;
    }
    else if (key < T->data) {
        //继续去左子树中查找目标元素
        return SearchBST(T->lchild, key);
    }
    else {
        //继续去右子树中查找目标元素
        return SearchBST(T->rchild, key);
    }
}

2、二叉排序树插入元素

二叉排序树中各个结点的值都不相等，因此新插入的元素一定是原二叉排序树没有的，否则插入操作会失败。此外插入新元素后，必须保证整棵树还是一棵二叉排序树。二叉排序树插入新元素的方法是：在树中查找新元素，最终查找失败时找到的位置，就是放置新元素的位置。例如在图 1 的二叉排序树中插入新元素 30，在树中查找 30，最终查找失败时找到的位置是结点 32 的左孩子，直接将 30 作为 32 的左孩子即可。图 3 二叉排序树插入新结点

编码实现向二叉排序树中插入新元素，可以参考下面的程序：

//向二叉排序树 T 中插入目标元素 e
Status InsertBST(BiTree* T, ElemType e) {
    //如果本身为空树，则直接添加 e 为根结点
    if ((*T) == NULL)
    {
        (*T) = (BiTree)malloc(sizeof(BiTNode));
        (*T)->data = e;
        (*T)->lchild = NULL;
        (*T)->rchild = NULL;
        return true;
    }
    //如果找到目标元素，插入失败
    else if (e == (*T)->data)
    {
        return false;
    }
    //如果 e 小于当前结点的值，表明应该将 e 插入到该结点的左子树中
    else if (e < (*T)->data) {
        InsertBST(&(*T)->lchild, e);
    }
    //如果 e 大于当前结点的值，表明应该将 e 插入到该结点的右子树中
    else
    {
        InsertBST(&(*T)->rchild, e);
    }
}

InsertBST() 函数本意是将指定元素插入到二叉排序树中，当二叉排序树不存在（为 NULL）时，此函数还能完成二叉排序树的构建工作。

作为实现动态查找表的树形结构，二叉排序树通常不会一次性创建好，而是一边查找一边创建，InsertBST() 就是实现此过程的函数。

3、二叉排序树删除元素

删除二叉排序树中已有的元素，必须确保整棵树还是一棵二叉排序树。假设被删除的元素是 P，删除的同时需要妥善处理它的左、右子树。根据结点 P 是否有左、右孩子，可以归结为以下 3 种情况：

P 是叶子结点：可以直接摘除，整棵树还是二叉排序树。例如，删除图 1 中的结点 32，它就是一个叶子结点，直接删除它并不会破坏二叉排序树的结构。
P 只有一个孩子（左孩子或右孩子）：若 P 是双亲结点（用 F 表示）的左孩子，直接将 P 的孩子结点作为 F 的左孩子；反之若 P 是 F 的右孩子，直接将 P 的孩子结点作为 F 的右孩子。例如，删除图 1 中的结点 29，它只有一个孩子结点 32。由于 29 是双亲结点 20 的右孩子，因此直接将 32 作为 20 的右孩子，这样做既删除了结点 29，整棵树还是二叉排序树。
P 有两个孩子：中序遍历整棵二叉排序树，在中序序列里找到 P 的直接前驱结点 S，将 P 结点修改成 S 结点，然后再将之前的 S 结点从树中摘除。(如果A有两个子节点，我们就以右子树内的最小节点取代A,从其右子树中找到最小值替代之)

在二叉排序树中，对于拥有两个孩子的结点，它的直接前驱结点要么是叶子结点，要么是没有右孩子的结点，所以删除直接前驱结点可以套用前面两种情况的实现思路。

例如，删除图 1 中的结点 20，它在中序序列里的直接前驱结点是 11，将 P 结点的值修改为 11，然后再根据情况 1 的实现思路，将之前的结点 11 直接从树中摘除。

编码实现在二叉排序树中删除某个元素，可以参考如下的程序：

//实现删除 p 结点的函数
Status Delete(BiTree* p)
{
    BiTree q = NULL, s = NULL;
    //情况 1，结点 p 本身为叶子结点，右孩子也为 NULL，用 NULL 直接替换 p 结点即可
    //情况 2,结点 p 只有一个孩子
    if (!(*p)->lchild) { //左子树为空，只需用结点 p 的右子树根结点代替结点 p 即可；
        q = *p;
        *p = (*p)->rchild;
        free(q);
    }
    else if (!(*p)->rchild) {//右子树为空，只需用结点 p 的左子树根结点代替结点 p 即可；
        q = *p;
        *p = (*p)->lchild;
        free(q);
    }
    //情况 3，结点 p 有两个孩子
    else {
        q = *p;
        s = (*p)->lchild;
        //遍历，找到结点 p 的直接前驱，最终 s 指向的就是前驱结点，q 指向的是 s 的父结点
        while (s->rchild)
        {
            q = s;
            s = s->rchild;
        }
        //直接改变结点 p 的值
        (*p)->data = s->data;
        //删除 s 结点
        //如果 q 和 p 结点不同，删除 s 后的 q 将没有右子树，因此将 s 的左子树作为 q 的右子树
        if (q != *p) {
            q->rchild = s->lchild;
        }
        //如果 q 和 p 结点相同，删除 s 后的 q（p） 将没有左子树，因此将 s 的左子树作为 q（p）的左子树
        else {
            q->lchild = s->lchild;
        }
        free(s);
        /*
         //左右节点都不空
        else 
        {
            s = p->rchild;
            /* the s without left child */
            if (!s->lchild)
                s->lchild = p->lchild;
            /* the s have left child */
            else 
            {
                /* find the smallest node in the left subtree of s */
                while (s->lchild) 
                {
                    /* record the parent node of s */
                    parent = s;
                    s = s->lchild;
                }
                parent->lchild = s->rchild;
                s->lchild = p->lchild;
                s->rchild = p->rchild;
            }
            *root = s;
        } */
    }
    return true;
}
//删除二叉排序树中已有的元素
Status DeleteBST(BiTree* T, int key)
{
    //如果当前二叉排序树不存在，则找不到 key 结点，删除失败
    if (!(*T)) {
        return false;
    }
    else
    {
        //如果 T 为目标结点，调用 Delete() 删除结点
        if (key == (*T)->data) {
            Delete(T);
            return true;
        }
        else if (key < (*T)->data) {
            //进入当前结点的左子树，继续查找目标元素
            return DeleteBST(&(*T)->lchild, key);
        }
        else {
            //进入当前结点的右子树，继续查找目标元素
            return DeleteBST(&(*T)->rchild, key);
        }
    }
}

二叉排序树的具体实现

总的来讲，实现二叉排序树的查找、插入和删除操作，可以参考如下的程序：

#include<stdio.h>
#include<stdlib.h>
#define ElemType int
#define KeyType int
typedef enum { false, true } Status;
/* 二叉排序树的节点结构定义 */
typedef struct BiTNode
{
    int data;
    struct BiTNode* lchild, * rchild;
} BiTNode, * BiTree;

//在 T 二叉排序树中查找 key
BiTree SearchBST(BiTree T, KeyType key) {
    //如果 T 为空，则查找失败，返回NULL；或者查找成功，返回指向存有目标元素结点的指针
    if (!T || key == T->data) {
        return T;
    }
    else if (key < T->data) {
        //继续去左子树中查找目标元素
        return SearchBST(T->lchild, key);
    }
    else {
        //继续去右子树中查找目标元素
        return SearchBST(T->rchild, key);
    }
}

//向二叉排序树 T 中插入目标元素 e
Status InsertBST(BiTree* T, ElemType e) {
    //如果本身为空树，则直接添加 e 为根结点
    if ((*T) == NULL)
    {
        (*T) = (BiTree)malloc(sizeof(BiTNode));
        (*T)->data = e;
        (*T)->lchild = NULL;
        (*T)->rchild = NULL;
        return true;
    }
    //如果找到目标元素，插入失败
    else if (e == (*T)->data)
    {
        return false;
    }
    //如果 e 小于当前结点的值，表明应该将 e 插入到该结点的左子树中
    else if (e < (*T)->data) {
        InsertBST(&(*T)->lchild, e);
    }
    //如果 e 大于当前结点的值，表明应该将 e 插入到该结点的右子树中
    else
    {
        InsertBST(&(*T)->rchild, e);
    }
}

//实现删除 p 结点的函数
Status Delete(BiTree* p)
{
    BiTree q = NULL, s = NULL;
    //情况 1，结点 p 本身为叶子结点，右孩子也为 NULL，用 NULL 直接替换 p 结点即可
    //情况 2,结点 p 只有一个孩子
    if (!(*p)->lchild) { //左子树为空，只需用结点 p 的右子树根结点代替结点 p 即可；
        q = *p;
        *p = (*p)->rchild;
        free(q);
    }
    else if (!(*p)->rchild) {//右子树为空，只需用结点 p 的左子树根结点代替结点 p 即可；
        q = *p;
        *p = (*p)->lchild;
        free(q);
    }
    //情况 3，结点 p 有两个孩子
    else {
        q = *p;
        s = (*p)->lchild;
        //遍历，找到结点 p 的直接前驱，最终 s 指向的就是前驱结点，q 指向的是 s 的父结点
        while (s->rchild)
        {
            q = s;
            s = s->rchild;
        }
        //直接改变结点 p 的值
        (*p)->data = s->data;
        //删除 s 结点
        //如果 q 和 p 结点不同，删除 s 后的 q 将没有右子树，因此将 s 的左子树作为 q 的右子树
        if (q != *p) {
            q->rchild = s->lchild;
        }
        //如果 q 和 p 结点相同，删除 s 后的 q（p） 将没有左子树，因此将 s 的左子树作为 q（p）的左子树
        else {
            q->lchild = s->lchild;
        }
        free(s);
    }
    return true;
}

//删除二叉排序树中已有的元素
Status DeleteBST(BiTree* T, ElemType key)
{
    //如果当前二叉排序树不存在，则找不到 key 结点，删除失败
    if (!(*T)) {
        return false;
    }
    else
    {
        //如果 T 为目标结点，调用 Delete() 删除结点
        if (key == (*T)->data) {
            Delete(T);
            return true;
        }
        else if (key < (*T)->data) {
            //进入当前结点的左子树，继续查找目标元素
            return DeleteBST(&(*T)->lchild, key);
        }
        else {
            //进入当前结点的右子树，继续查找目标元素
            return DeleteBST(&(*T)->rchild, key);
        }
    }
}

//中序遍历二叉排序树
void INOrderTraverse(BiTree T) {
    if (T) {
        INOrderTraverse(T->lchild);//遍历当前结点的左子树
        printf("%d ", T->data);     //访问当前结点
        INOrderTraverse(T->rchild);//遍历当前结点的右子树
    }
}

//后序遍历，释放二叉排序树占用的堆内存
void DestroyBiTree(BiTree T) {
    if (T) {
        DestroyBiTree(T->lchild);//销毁左孩子
        DestroyBiTree(T->rchild);//销毁右孩子
        free(T);//释放结点占用的内存
    }
}

int main()
{
    int i;
    int a[10] = { 41,20,11,29,32,65,50,91,72,99 };
    BiTree T = NULL;
    for (i = 0; i < 10; i++) {
        InsertBST(&T, a[i]);
    }
    printf("中序遍历二叉排序树：\n");
    INOrderTraverse(T);
    printf("\n");
    if (SearchBST(T, 20)) {
        printf("二叉排序树中存有元素 20\n");
    }
    printf("删除20后，中序遍历二叉排序树：\n");
    DeleteBST(&T, 20);
    INOrderTraverse(T);
    //后续遍历，销毁整棵二叉排序树
    DestroyBiTree(T);
}

以图 1 为例，程序执行结果为：

中序遍历二叉排序树： 11 20 29 32 41 50 65 72 91 99 二叉排序树中存有元素 20 删除20后，中序遍历二叉排序树： 11 29 32 41 50 65 72 91 99

总结

二叉排序树是一种实现动态查找表的树形存储结构。同一张查找表中，元素的排序顺序不同，最终构建出的二叉排序树也不一样。例如，{45，24，53，12，37，93} 和 {12，24，37，45，53，93} 是同一张动态查找表，只是元素的排序顺序不同，它们对应的二叉排序树分别为：

图 4 不同形态的二叉排序树

左侧二叉排序树表示的是 {45，24，53，12，37，93}，右侧二叉排序树表示的是 {12，24，37，45，53，93}。二叉排序树的查找性能和整棵树的形态有关。以图 4 为例，假设查找表中元素被查找的概率是相等的（都为1/6），左侧二叉排序树的查找性能用平均查找长度（ASL）表示：

ASL = 1/6 * (1+2+2+3+3+3) = 14/6

右侧二叉排序树的查找性能为：

ASL = 1/6 * (1+2+3+4+5+6) = 21/6

ASL 值越小，查找的性能就越高。显然，图 4 左侧二叉排序树的查找性能更高。也就是说，一张动态查找表往往对应着多棵二叉排序树，当表中元素的查找概率相同时，二叉排序树的层数越少，查找性能越高。

数据结构-特殊树之二叉搜索树BST