二叉树

1、二叉树定义

如果每个结点的子结点的数目最多为2个，则该树称为二叉树。

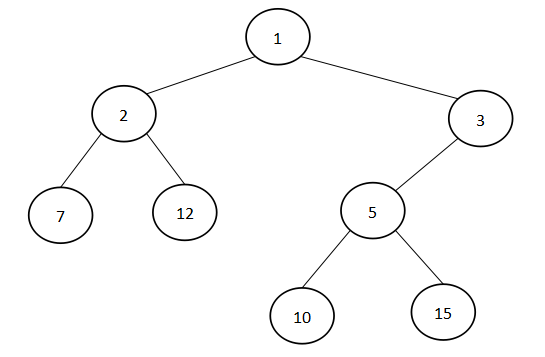
特点：

• 每个结点最多有两颗子树，所以二叉树中不存在度大于2的结点。
• 左子树和右子树是有顺序的，次序不能任意颠倒。
• 即使树中某结点只有一棵子树，也要区分它是左子树还是右子树。

满二叉树：所有分支结点都有两个子结点，并且所有叶结点都在最后一层。

• n层的满二叉树：结点个数为 $1+2+4+...+2^n = 2^{n+1} - 1$
• 按上到下、左到右对结点编号：
  • 第i层编号为 $2^{i-1}$ 开始，到 $2^i - 1$ 结束
  • 对编号k的结点，其左子孩子编号为 2k, 右孩子为2k+1
  • 对编号k的结点，其父亲（除根外）编号为k/2

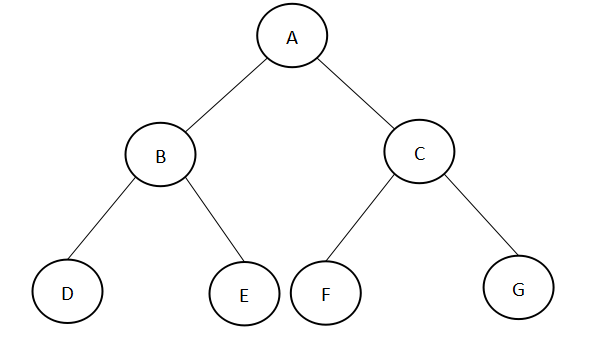
完全二叉树：每个结点的位置与满二叉树的结点位置一样（但不一定满）。

2、二叉树存储

对于完全二叉树，可以用一维数组进行存储，根据结点的父子关系就可以正常访问。

例子：上面的满二叉树

char v[10] = "-ABCDEFG";

对于非完全二叉树，如果不想浪费空间（没有子结点的位置也被占用），可以继续用邻接表方式存储。

3、遍历方式

二叉树的每个结点，加上其左孩子（子树）、右孩子（子树），一共三个部分，在遍历的时候，可以按照不同的次序进行遍历（孩子必须先左后右），共有三种：

• 先序：根 左 右
• 中序：左 根 右
• 后序：左 右 根

对例子满二叉树来说：

• 先序：A B D E C F G
• 中序：B D E A C F G
• 后序：B D E C F G A

树的遍历

树上 DFS

在树上 DFS 是这样的一个过程：先访问根节点，然后分别访问根节点每个儿子的子树。

可以用来求出每个节点的深度、父亲等信息。

二叉树 DFS 遍历

先序遍历

按照 根，左，右 的顺序遍历二叉树。

实现

void preorder(BiTree* root) {
  if (root) {
    cout << root->key << " ";
    preorder(root->left);
    preorder(root->right);
  }
}

中序遍历

按照 左，根，右 的顺序遍历二叉树。

实现

void inorder(BiTree* root) {
  if (root) {
    inorder(root->left);
    cout << root->key << " ";
    inorder(root->right);
  }
}

后序遍历

按照 左，右，根 的顺序遍历二叉树。

实现

void postorder(BiTree* root) {
  if (root) {
    postorder(root->left);
    postorder(root->right);
    cout << root->key << " ";
  }
}

反推

已知中序遍历序列和另外一个序列可以求第三个序列。

1. 前序的第一个是 root，后序的最后一个是 root。
2. 先确定根节点，然后根据中序遍历，在根左边的为左子树，根右边的为右子树。
3. 对于每一个子树可以看成一个全新的树，仍然遵循上面的规律。

树上 BFS

从树根开始，严格按照层次来访问节点。

BFS 过程中也可以顺便求出各个节点的深度和父亲节点。

树的层序遍历

树层序遍历是指按照从根节点到叶子节点的层次关系，一层一层的横向遍历各个节点。根据 BFS 的定义可以知道，BFS 所得到的遍历顺序就是一种层序遍历。但层序遍历要求将不同的层次区分开来，所以其结果通常以二维数组的形式表示。

例如，下图的树的层序遍历的结果是 [[1], [2, 3, 4], [5, 6]]（每一层从左向右）。