树的定义、存储

一、树的定义

树是一种非线性的数据结构，是由n（n>=1）个有限结点组成一个具有层次关系的集合。把它叫做“树”是因为它看起来像一棵倒挂的树，也就是说它是根朝上、叶朝下的。

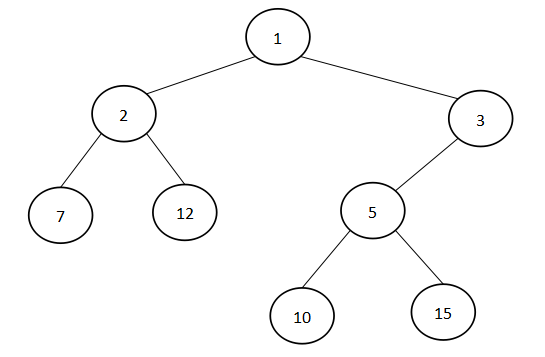
父子关系:

• 每个结点(node)有零个或多个子结点(child)
• 每一个非根结点有且只有一个父结点(parent)
• 没有父结点的结点称为根结点(root)，有且仅有一个根结点

树与图：图是点和边的集合，树是点和父子关系（边）的集合。

树 <=> n个顶点、n-1条边的连通图。

• 无环
• 连通

子树：

• 每个结点都可以看成一个树，非根结点的树，称为子树。
• 子树互相独立

空树：空集合也是树，称为空树。

二、树的存储

树的核心应用就是遍历访问，出于父子关系的特点，必须要考虑两种访问场景：

• 从父结点出发访问子结点
• 从子结点出发访问父结点

因此为了支持这两种场景（甚至两者都有），就产生了三种基本的（邻接表）存储方式。

• 孩子表示法：每个结点存储它所有孩子的的位置（用链表或动态数组）
• 父亲表示法：每个结点存储父亲的位置，可以快速访问到
• 父亲孩子表示法：每个结点即存储父亲位置，也存储所有孩子的位置

2.1 孩子表示法

每个节点存储孩子列表，方便从上往下遍历。

方案：

• 用vector g[N]， g[x]里存储的是孩子列表
• 如果孩子有其它信息，比如边权，则可使用结构体

优缺点：

• 从上往下遍历很方便
• 找父亲和祖先都比较麻烦

2.2 父亲表示法

每个结点存储父亲的位置，方便能从下往上遍历。

int fa[N];//下标x是节点编号，fa[x]是其父亲的编号

优缺点：

• 结点能快速找到其父亲，复杂度为O(1)
• 从结点往上找根结点也比较容易，复杂度为O(logn)
• 从结点找孩子比较麻烦，要循环判定，复杂度为O(n)

2.3 父亲孩子表示法

每个节点即存储父亲，也存储孩子列表，这样就能即支持从下往上遍历，也支持从上往下遍历。

可用结构体来存储每个节点的信息，也可以在孩子表示法基础上，再用fa[N]数组来存储父亲。

三、树的基本概念

1、根节点

树有一个根节点，从根节点可以遍历到所有其它节点。

有根树是已经指定根节点的树，无根树是没有指定根节点的树。

孩子表示法可以用来表示无根树，父亲表示法只能用来表示有根树。

2、父亲数组

指定根节点后，就可以得到父亲数组，用来从某个节点遍历到根节点。

可在dfs时通过传入参数_fa来赋值给每个节点：

void dfs(int x, int _fa) {
  fa[x] = _fa;
  for(...)
    dfs(y, x);
}

3、深度（距离）

指每个节点到根的路径上点的个数，一般根的深度为1。

树的高度：树上所有点的最大深度。

可在dfs时通过传入参数_dep来赋值给每个点：

void dfs(int x, int _dep) {
  dep[x] = _dep;
  for(...)
    dfs(y, _dep+1);
}

4、带权深度

节点到根的路径上的边权之和，类似dep[]，可在dfs时传入参数_len赋值：

void dfs(int x, int _len) {
  len[x] = _len;
  for(...)
    dfs(y, _dep+w);//w是<x, y>的边权
}

5、子树大小

节点x及其子树里节点的个数之和，称为子树大小，一般用size[N]表示。

对于树边<x, y>，y点给x的子树大小贡献了size[y]个。

因此可在dfs调用之后递推累加：

void dfs(int x) {
  size[x] = 1;
  for(...) {
    dfs(y);
    size[x] += size[y];
  }
}

6、子树权值和

每个节点有一个权值w[N]，子树权值和表示该点及其子树所有节点权值的和。

定义sum[N]表示子树权值和，则对于边<x, y>，y给x贡献了sum[y]。

类似子树大小：

void dfs(int x) {
  size[x] = w[x];
  for(...) {
    dfs(y);
    sum[x] += sum[y];
  }
}

7. LCA

树上两个点x、y，各自往根的路径相交的点里面层级最大的，称之为LCA（最大公共祖先）。

根据父亲数组fa[N]和层级数组dep[N]，就可以计算出LCA。

朴素算法一：

• 首先将层级大的点往上跳，直到层级相同
• 如果相等即为LCA
• 否则两个点同时往上跳，直到相等，即为LCA

朴素算法二：

• 将x到根的点都标记起来
• 从y开始往上跳，遇到第一个标记的点，即为LCA

例题与练习

CCFPS01D01 树的儿子个数

CCFPS01D02 树的儿子个数2

CCFPS02D04 子树之和