动态规划入门

例题
CCFPB01E03爬楼梯
YBTJ1281最长上升子序列
P2403信封错排
P204【基础】最大部分和（连续部分和）

1、什么是动态规划

动态规划是一种数学方法，一般应用于多决策过程，用来求最优化的问题。

动态规划通过定义问题的状态以及状态之间的关系，来拆分问题，使得问题能够以递推的方式被解决。

如何观察问题，定义问题的状态，从而对问题进行拆分，这是动态规划的关键之处。

另一方面，对于一个问题，以什么作为状态，并不固定，需要有丰富的经验、很强的观察能力和分析能力。这也是大家觉得动态规划比较难掌握的地方。

2、动态规划怎么用

2.1 定义状态

问题：最长递增子序列的长度

求一个数列的最长上升递增子序列（LIS）的长度。
例如：1 7 2 8 3 4，
递增子序列有：1 7, 1 8, 1 7 8, 1 2 3 4,  2 3 4等等
最长递增子序列为 1 2 3 4， 长度为4
第二长的子序列有：1 2 3 、 1 7 8等，长度为3

问题是什么？子问题又是什么呢？怎么叫通过定义状态来拆分问题？

我们将问题换一种说法：

设Fk为数列中第k项元素为结尾元素的最长递增子序列的长度
求F1...Fn的最大值

例如F5为 1 7 2 8 3的最长递增子序列的长度，结果为3
F4为 1 7 2 8 的最长递增子序列的长度，也是3

这个问题与原问题等价，但这么描述就可以拆分问题。

对于Fk来说，F1...Fk-1都是Fk的子问题：因为，以第k项结尾的LIS包含着以第1...k项中某项结尾的LIS。

描述“设Fk为....”，就叫做对状态的定义，Fk叫做状态，对应的k是我们提取的维度。

之所以叫状态而不是叫问题，一是避免与原问题混淆，二是因为这是一个数学定义。

2.2 状态转移方程

定义了状态，也即定义了问题与子问题，F1...Fk-1都是Fk的子问题。

接下来，就可以拆分问题，如何将Fk拆分为子问题（的组合）呢？

实际就是找到状态与状态之间的关系式，让Fk可以通过F1...Fk-1运算得到。

F1=1（边界）
Fk=max(Fi)+1, 1<=i<k且Ai < Ak

以上，由于Fk的结尾元素为Ak，则Ak必须大于Ai。

2.3 构造最优解

由状态转移方程，就可以计算出所有的状态。

注意：状态并不一定是最终的最优解，有时候还要通过状态再进行计算，来构造出问题的最优解。

3、动态规划的实现

3.1 图表实现

定义状态和状态转移方程以后，就可以根据状态画出图（或表格），然后按照拓扑排序依次更新每个状态的值。

例如：对于1 7 2 8 3 4，找LIS

a[] 1 7 2 8 3 4
Fi/dp[] 1 2 3 3 4
b[] 1 5
(b[]表示记录是从前面哪个元素来的)

上图从左到右填充，例如：

  • 首先填写F1，值为1
  • 然后填写F2，F1+1 = 2
  • F3，F1+1 = 2
  • F4，max(F1,F2,F3)+1 = 3
  • F5，max(F1,F3)+1 = 3
  • F6，max(F1,F3,F5)+1 = 4

3.2 递归编程

显然，可以用递归函数的方式来编写以上状态转移方程。

int f(int k) {
  if(k==1) return 1;
  //序列的数组从下标1开始
  int r=0;
  for(int i=1; i<k; i++) {
    if (a[i] < a[k]) r=max(r, f(i)+1);
  }
  return r;
}

需要注意的是，递归会产生大量的重复计算，例如：

  • f(k) -> f(k-1)、f(k-2)...f(1)
  • f(k-1) -> f(k-2)...f(1)
  • ......

这是一个树，总共结点规模约为k^k。

这样的运算量显然有问题，于是要把这些重复的计算存储起来，下次用到的时候重用。

3.3 记忆递归

假设用一个状态数组dp[N]存储前面运算过的状态，则代码变成：

int dp[N];
int f(int k) {
  if(k==1) return 1;
  int r=0;
  for(int i=1; i<k; i++) {
    int tmp;
    if(dp[i]) tmp = dp[i];
    else tmp = dp[i] = f(i);

    if (a[i] < a[k]) r=max(r, tmp+1);

  }
  return r;
}
f(1),f(2),...,f(n)
    f(n) (f(1)...f(n-1))
    dp[1]=1;
dp[2]=dp[1]+1;a[1]<a[2]

3.4 递推

用数组存储每次运算好的状态，然后依次往后递推。

int dp[N];
int f(int k) {
  dp[1] = 1;
  for(int i=2; i<=k; i++) {
    int m = 0;
    for(int j=1; j<i; j++) {
      if(a[i] > a[j]) m=max(m, dp[j]+1);
    }
    dp[i]=m;
  }
  return dp[k];
}

4、动态规划的特征

对问题进行分析，具备以下三个特性的，比较适合使用动态规划。

4.1 最优子结构

问题的最优解就是找到此问题的最优状态。

"每个最优状态可以根据前面某个（或某些）状态直接得到"

这个性质就叫做“最优子结构”。

最优子结构表示问题（状态）的最优解包含其子问题（状态）的最优解。

4.2 无后效性

"每个最优状态可以根据前面某个（或某些）状态直接得到"

“而不管之前这些状态是怎么得到的”

后面这个性质，称之为“无后效性”。

无后效性表示计算最优状态的时候，不需要关注前面的状态是怎么得到的（不受影响），只需要用到它们的值即可。

4.3 子问题重叠

在状态转移方程计算的时候，有大量的子问题被重复运算。

动态规划要求所有的子问题都只需要解决依一次，存储起来供下次重用。

如果子问题重叠性不强，用动态规划的收益就不大，必要性就不强。

5、动态规划与其它算法的关系

首先，递推、递归是动态规划编程实现比较常用的技巧。

对于一个问题：

  • 首选模拟、枚举、搜索
  • 问题可分解成独立子问题的，用分治
  • 最优状态可由上一个最优状态得到的，用贪心
  • 最优状态可由前面某个(些)状态得到而不管之前状态是如何得到的，用动态规划

例题和练习

演示-走楼梯

CCFPB01E03 爬楼梯

####　一、实验目标 有一座高度是n级台阶的楼梯，从下往上走，每跨一步只能向上1级或者2级台阶。请问一共有多少种走法。

输入样例1：

10

输出样例1：

89

二、分析

1、模拟
  • 从最下走到第一级台阶，有1种走法
  • 从最下走到第二级台阶，有2种走法:
    • 走法一：先到第一级，再从第一级到第二级
    • 走法二：直接到第二级
  • 从最下走到第三级台阶，有3种走法：
    • 走法一：先到第一级，再跨两级直接到第三级
    • 走法二：先经过第一级到第二级，再到第三级
    • 走法三：先到第二级，再跨一级到第三级

注意到第三级台阶的走法，可以描述成两种选择：

  • 选择一：先到第一级，再跨2步到第三级，走法数是到第一级的走法数
  • 选择二：先到第二级，再到1步第三级，走法数是到第二级的走法数

根据加法原理：

到第三级的走法数 = 到第一级的走法数 + 到第二级的走法数

2、思路分析

根据以上模拟，抽象出一个概念：

对于任何一级台阶，假设级数为n，想要走到第n级，必须先走到第n-2级或者第n-1级，然后才能通过走1步或2步的方式走到第n级。

  • 如果先到第n-2级，那么走法数就是到第n-2级的走法数
  • 如果先到第n-1级，那么走法数就是到第n-1级的走法数 分析：

将台阶的级数作为维度（下标） 从下网上走到第i级（维度）台阶的走法数，作为状态（用dp[i]表示)） 一般维度作为下标，定义一个状态，分析是否具有无后效性，然后找出状态转移方程。

无后效性：状态的转移与如何到达该状态无关，也即“未来与过去无关”。 例如：

从第一级走2步到第三级，这个转移与如何到达第一级无关。 从第二级走1步到第三级，这个转移也与如何到达第二级无关。 状态转移方程：

dp[1] = 1, dp[2] = 2
dp[i] = dp[i-2] + dp[i-1]， 对于i>2

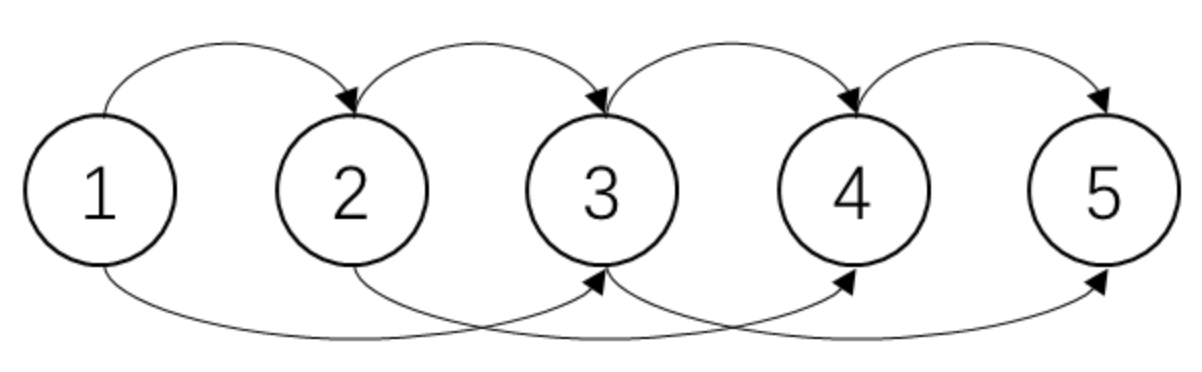
将状态转移的方式画出一个图，就是一张有向无环图： image

动态规划本质上就可以理解成状态在有向无环图上的递推过程。

3、实现方法

对于动态规划的实现，可以用递归，也可以用递推，可根据具体情况选用不同的方法。

需要注意的是，状态（值）的变化一定要遵循状态的拓扑序，以下两种都可以：

dp[i] = dp[i-2] + dp[i-1]
dp[i+1] += dp[i], dp[i+2] += dp[i]

本题分别用f1（递归）、f2（递归＋记忆）、f3（递推1）、f4（递推2）四个函数来实现求第n级的走法数。

4、实现代码
#include <iostream>
using namespace std;

int f1(int n) {
  if(n<=2) return n;
  return f1(n-1) + f1(n-2);
}

int dp[100];
int f2(int n) {
  if(n<=2) return n;
  if(dp[n]) return dp[n];
  return dp[n] = f2(n-1) + f2(n-2);
}

int f3(int n) {
  int a=1, b=2;
  for(int i=3; i<=n; i++) {
    int tmp = a+b;
    a = b;
    b = tmp;
  }
  return b;
}

int f4(int n) {
  dp[1]=1, dp[2]=1;
  for(int i=1; i<n; i++) {
    dp[i+1] += dp[i];
    dp[i+2] += dp[i];
  }
  return dp[n];
}

int main() {
  int n;
  cin>>n;
  //cout<<f1(n)<<endl;
  //cout<<f2(n)<<endl;
  //cout<<f3(n)<<endl;
  cout<<f4(n)<<endl;
  return 0;
}

最大递增子序列

一、实验目标

给定一个长度为N的数列，求这个数列的最长递增子序列（LIS）的长度。

例如：1 7 2 8 3 4的LIS为1 2 3 4，长度为4

输入样例：第一行是n，第二行为n个数

6
1 7 2 8 3 4

输出样例：

4

输入样例2：

6
1 7 2 3 8 3

输出样例2：

4

数据规模：1<=N<1000

请使用动态规划实现。

二、分析

理解问题，设计状态，找出状态转移方程。

维度：数列的下标 状态：设dp[k]为数列中第k项元素作为结尾的LIS的长度 状态转移方程：

dp[1] = 1
dp[k] = max(dp[i])+1, 1<=i<k 且a[i]<a[k]

解释：

dp[i]的结尾元素是a[i]，dp[k]的结尾元素为a[k]，即dp[k]是前面的某个dp[i]，加上a[k]形成的LIS的长度 找所有1<=i<k且a[i]<a[k]的i，求max(dp[i]+1)，即为dp[k] 最后输出的，是所有dp的最大值

三、实验步骤

请自己实现以下步骤：

  1. 数据定义：N、a[N]、dp[N]
  2. 输入n和a[n]
  3. 递推计算dp
  4. 输出

四、扩展理解

如果定义状态：设dp[k]为前面k项的LIS的长度可以吗？

对于前面k项的LIS，可能会有多个结尾元素，有些大于a[k+1]，有些小于a[k+1]，会有后效性。

练习-信封错排

信封错排

n封信放入n个信封，要求全部放错，共有多少种放法。

请你用动态规划分析题目，设计状态，找出状态转移矩阵，然后编程实现。

输入样例：一个数字n

5

输出样例：错排的放法数目

44

数据范围：1<=N<=20

二、分析

1、理解题目

k封信放入k个信封，错排的放法数。

把信封理解成数组下标，信理解成数组的值，则问题转化为：

n个不相等元素的数组，每个位置都不等于其下标，有几种。 用什么做维度？k

状态是什么？dp[k]：k个元素的错排总数

状态方程是什么？

2、状态转移方程

注意：以下的n不是题目输入的n，只是一个符号。

假设一种错排方案里，n位置放的是k元素，现在看k位置放的是什么值：

k位置放的是n元素，则除n、k位置之外的n-2个位置要全部错排，即dp[n-2] k位置放的是m元素（不等于n），将n和k位置交换，则k位置放了k，n位置放了m，也就是除k以外的位置要全部错排，即dp[n-1] 根据加法原理，以上两种的和为 dp[n-1] + dp[n-2]

又，k元素的选值有n-1种，于是总的状态转移方程：

dp[n] = (n-1) * (dp[n-1] + dp[n-2])
三、实验步骤

请自己实现以下步骤：

  1. 接收输入n，定义dp数组
  2. 递推实现动态规划
  3. 输出

演示-最大子段和

一、实验目标

P204 【基础】最大部分和（连续部分和）

洛谷1115

给出一段序列，选出其中连续且非空的一段使得这段和最大。

输入样例：第一行n（长度），第二行n个数据

7
2 -4 3 -1 2 -4 3

输出样例：最大字段和，子段最小长度为1

4

样例说明：最大的字段和为4， 该字段为 3 -1 2

数据范围：

每个元素绝对值<= 10000
40%的数据：n<=2000
100%的数据：n<=200,000

本题要求用动态规划实现。

二、分析

1、理解题目

分析样例数据：

下标 1 2 3 4 5 6 7
序列 2 -4 3 -1 2 -4 3
前缀和 -2 1 0 -2 1
如果定义了前缀和p[i]=a[1]+...+a[i]p[i] = a[1]+...+a[i]，那么有子段和s[i][j]=p[j]−p[i]s[i][j] = p[j] - p[i]，表示下标为i+1， ... ，ji+1，\space ... \space，j的子段和。

显然，如果p[j]固定的话，那么p[j] - p[i]最大，必然p[i]为最小。

于是定义状态：设dp[j]为前j个元素里最小的前缀和p[i],0≤i≤jp[i], 0\le i\le j，

注意：序列从1开始，但前缀和0开始，令p[0] = 0

模拟如下：

下标 0 1 2 3 4 5 6 7
序列 - 2 -4 3 -1 2 -4 3
前缀和 0 -2 1 0 -2 1
最小前缀和 0 -2 -2
最大字段和 2 0 3 2 4 0 3

最大子段和为p[5] - dp[2] = 4，子段为3 -1 2

2、状态设计

状态：设dp[j]为前j个元素里最小的前缀和p[i], 0<=i<=j，

状态转移方程为：

dp[0] = 0
dp[j] = min(dp[j-1], p[j])

最大字段和为max(p[j] - dp[j-1]), 1<=j<=n，

注意：

题目提示每个元素绝对值<=10000，也即max初始值为-10000 为什么减去dp[j-1]，因为题目要求最少要一个元素。 如果要找出序列，就要记录dp[j]在哪个下标

3、换一种状态定义

定义状态：设dp[i]为第i个元素为结尾的最大子段和

那么对于dp[i]，要么是a[i]自己（从头计算），要么是dp[i-1]+a[i]

于是状态转移方程：

dp[1] = a[1]
dp[i] = max(a[i], dp[i-1]+a[i])

最后计算dp序列的最大值，即为总的最大子段和。

三、实验步骤

请分别实现两种动态规划思路：

  1. 数据定义和输入
  2. 第一种思路f1()
  3. 第二种思路f2()

四、参考代码

#include <iostream>
using namespace std;

const int N=200005;
int n;
int a[N];
int p[N];
int dp[N];

void f1() {
  for(int i=1; i<=n; i++)
    p[i] = p[i-1] + a[i];
  
  for(int i=1; i<=n; i++) {
    dp[i] = min(dp[i-1], p[i]);
  }
  
  int maxx = -10001;
  for(int i=1; i<=n; i++) {
		int tmp = p[i] - dp[i-1];
    if(tmp>maxx) {
      max = tmp;
    }
  }
  cout<<max;
}

void f2() {
  dp[1] = a[1];
  for(int i=2; i<=n; i++)
    dp[i] = max(dp[i-1]+a[i], a[i]);
  
  int maxx = dp[1];
  for(int i=2; i<=n; i++)
    if(dp[i]>maxx) {
      maxx = dp[i];
    }
  cout<<maxx;
}

int main() {
  cin>>n;
  for(int i=1; i<=n; i++)
    cin>>a[i];

  f1();
  //f2();
  return 0;
}

  1. 关于
  2. 联系我们
  3. 隐私
  4. 服务条款
  5. 版权申诉
  6. Language
  7. 兼容模式
  8. 主题
  3. Worker 0, 27ms
  4. Powered by Hydro v4.19.1 Community