分治

例题：

题目
P27 快速幂

1、分治思想

分治的基本思想是将一个规模为 $n$ 的问题分解为多个规模较小的子问题，这些子问题与原问题相同又互相独立，每个子问题又递归分解，直到子问题求解完成，然后再将子问题的解合并得到原问题的解。

2、理解分治思想

分治思想的场景：当前问题规模较大不好求解，而子问题在问题规模降到某一阀值时比较容易求解，因此通过递归分解子问题得到子问题的解，再将解逐层合并回来。

适合问题的主要特征：

1. 规模较小（到一定阀值）时容易求解。
2. 具有最优子结构性质（可分解为k个相同的子问题）
3. 子问题的解可以合并回来
4. 子问题相互独立（不含公共的子问题）

如果第3点不满足则不能使用分治，一般可用贪心或动态规划。

如果第4点不满足，则用分治的话就会产生很多重复运算，一般用动态规划会更好。

3、分治的核心步骤

分治的三个核心步骤：

• 分解子问题Divide
• 求解子问题Conquer
• 合并子问题的解Combine

由于需要持续分解，因此分治一般都采用递归的方式进行，问题的分解自上而下，解的合并自下而上。

伪代码如下：

void 分解与合并(问题P) {
  if (问题规模 <= 规模阀值)  return 求解(P);
  
  分解成k个子问题P1...Pk;
  
  for(i=1; i<=k; i++)
    解yi = 分解与合并(Pi);
  return 合并(y1, y2, ..., yk);
}

4、简单案例

题目
P591 查找给定的K

问题：在一个单调序列里找一个数x，输出下标，没有找到就返回-1。

枚举法：循环比较

二分法：二分逼近

分治法怎么做呢？

分析：

问题规模为n，当问题规模到1时，自然求解 每次将问题分成两个子问题，通过递归函数传入参数L和R的方式进行分解 此问题的解无需合并，直接返回即可

思考

分治与递归 分治与二分 分治与动态规划 分治的经典应用很多，例如归并排序、快速排序等，更多的将在以后再提及。

归并排序

例题：

题目
CCFPB06D12 排序

1. 归并排序

归并排序（Merge-sort）是利用归并的思想实现的排序方法，该算法采用经典的分治（divide-and-conquer）策略。

将大数组的排序问题分(divide)成小数组的排序问题然后递归求解，而治(conquer)的阶段则将分的阶段得到的有序子序列按顺序合并在一起，即分而治之。

1.1 算法描述

• 归并排序分的过程是通过递归函数，将序列每次尽量对半分，直到只剩一个数（一个数视为有序）为止。
• 治的过程则是合并，将两个小的有序部分合并为大的有序部分。

1.2 图示

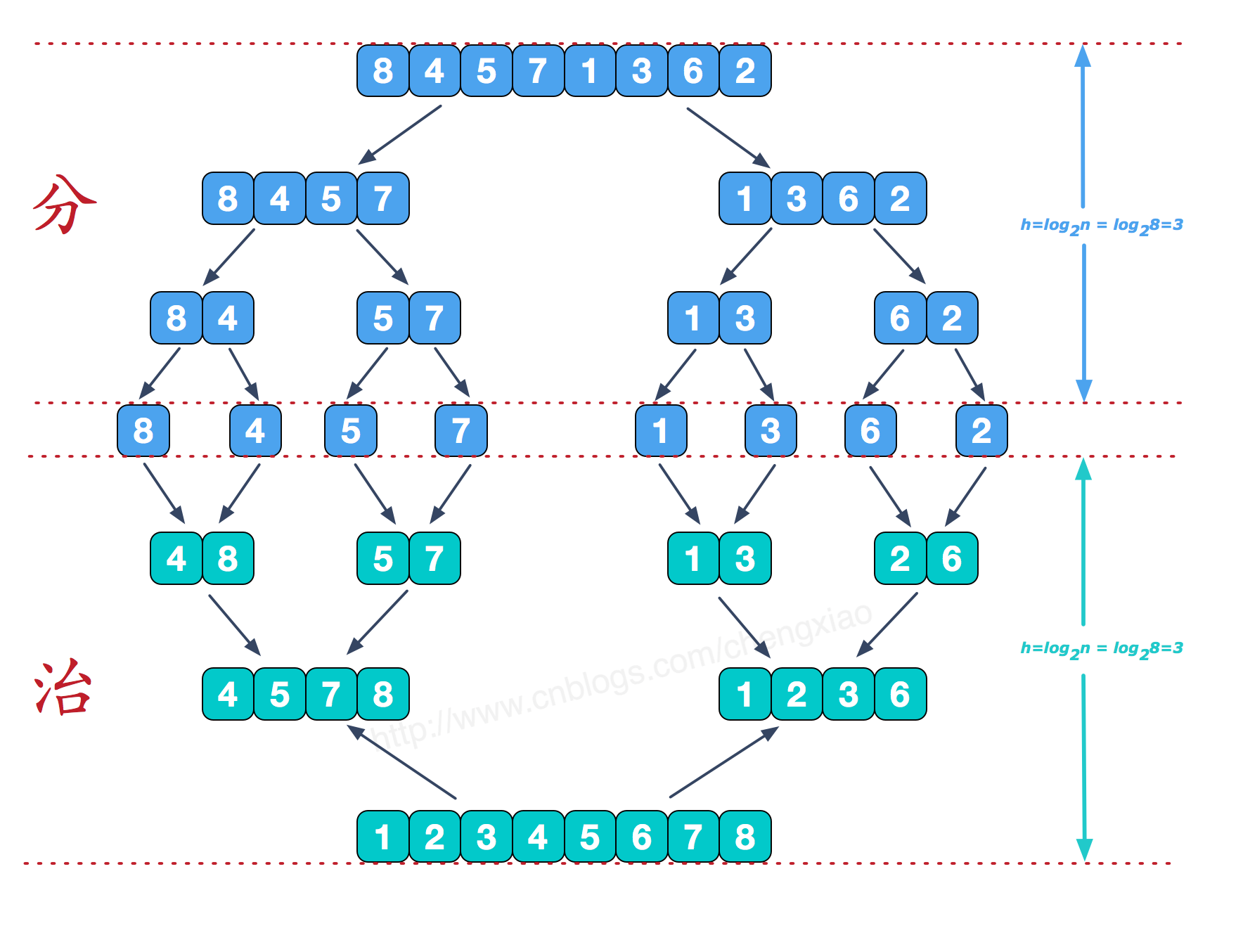
void mergeSort(int L, int R) {
  if(L >= R) return;
  int mid = (L+R)/2;
  mergeSort(L, mid);
  mergeSort(mid+1, R);
  merge(L, mid, R);
}

1.3 具体的合并过程图示

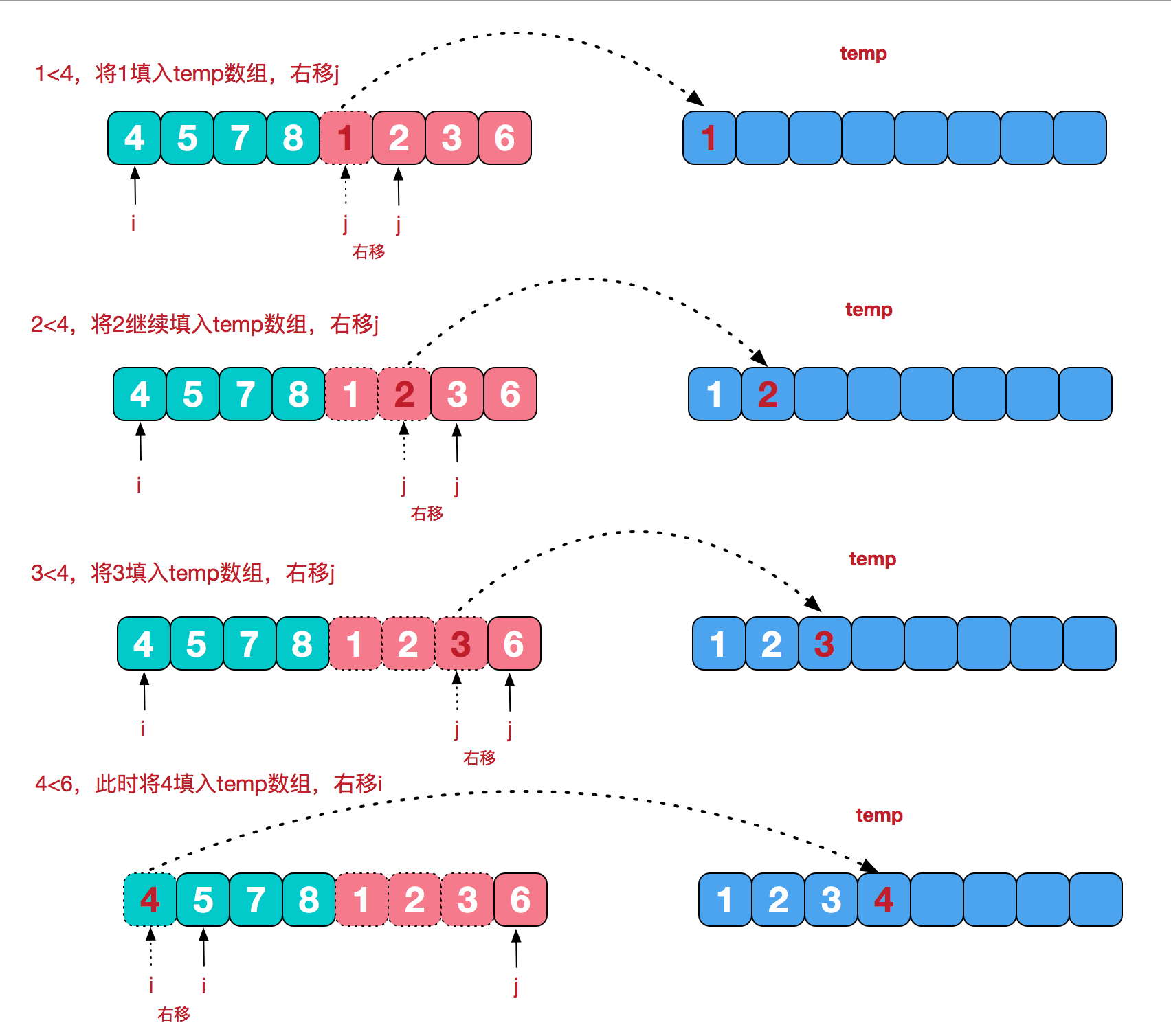
void merge(int L, int mid, int R) {
  int i=L, j=mid+1, idx=L;
  while(i<=mid && j<=R) {
    if(a[i]<=a[j]) {
      temp[idx++] = a[i];
      i++;
    } else {
      temp[idx++] = a[j];
      ans += mid-i+1;
      j++;
    }
  }
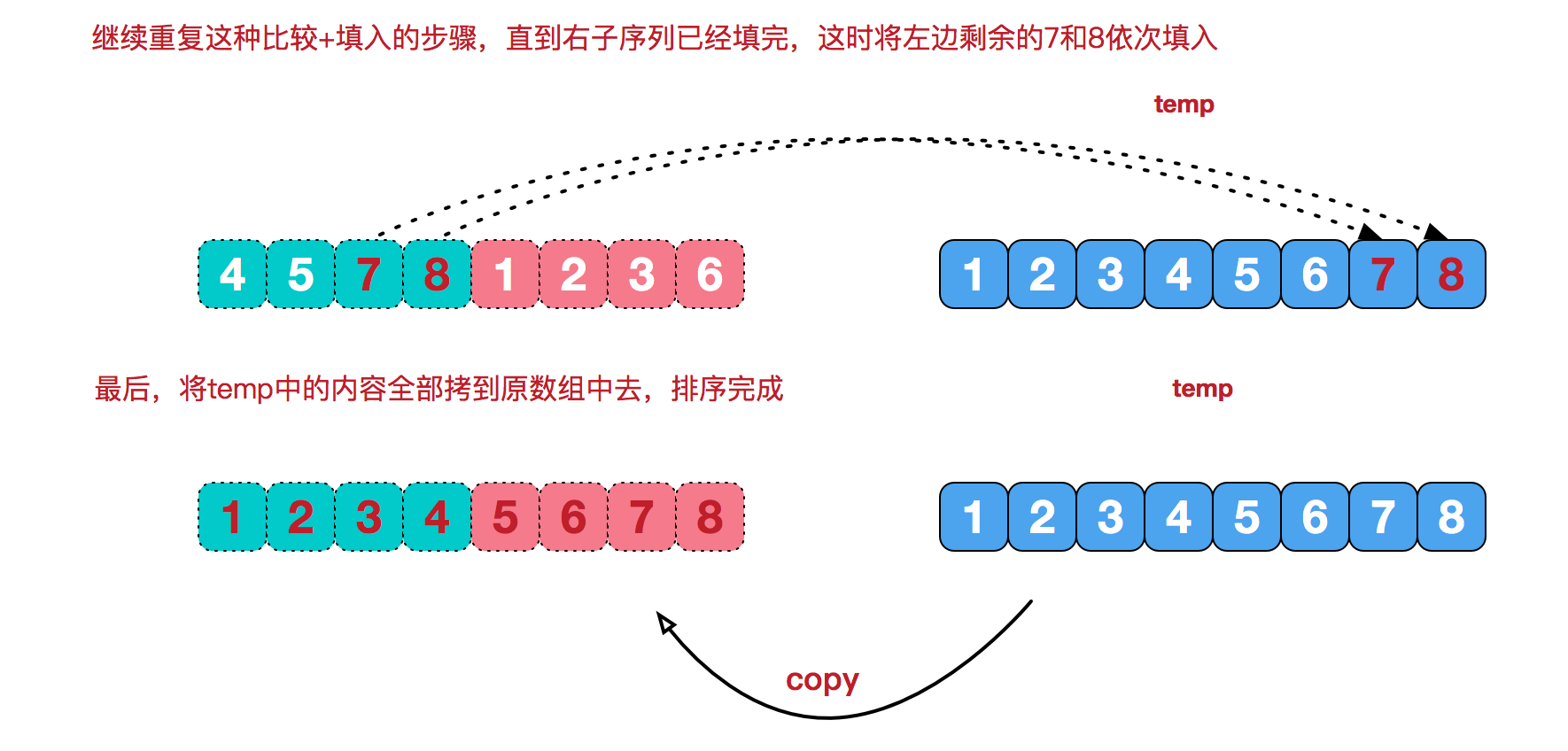
  while(i<=mid) {
    temp[idx++] = a[i];
    i++;
  }
  while(j<=R) {
    temp[idx++] = a[j];
    j++;
  }
  
  for(int i=L; i<=R; i++)
    a[i] = temp[i];
}

2、逆序对问题

练习题
YBT1311求逆序对
YBTJ1328【例7.7】光荣的梦想

设 A 为一个有 n 个数字的有序集 (n>1)，如果存在正整数 i、j 使得 1 ≤ i < j ≤ n 而且 A[i] > A[j]，则 <A[i], A[j]> 这个有序对称为 A 的一个逆序对，也称作逆序数，可在归并排序的合并过程中顺便求出。

void merge(int L, int mid, int R) {
  int i=L, j=mid+1, idx=L;
  while(i<=mid && j<=R) {
    if(a[i]<=a[j]) {
      temp[idx++] = a[i];
      i++;
    } else {
      temp[idx++] = a[j];
      ans += mid-i+1;//a[i] > a[j]，a[i]后面的都>a[j]，因此个数为mid - i + 1
      j++;
    }
  }
  while(i<=mid) {
    temp[idx++] = a[i];
    i++;
  }
  while(j<=R) {
    temp[idx++] = a[j];
    j++;
  }
  
  for(int i=L; i<=R; i++)
    a[i] = temp[i];
}

快速排序算法

快速排序（Quick-sort）利用二分思想，完成数列的排序操作。

快速排序通过在待排序序列中选取基准值，再将数列调整为以基准值位置为界，一侧比基准值小，另一侧则比基准值大，然后递归两侧执行同样操作，即可完成排序。

算法分析

1.获取基准值pivot

获取基准值有很多种方法，简单起见可选取待排序序列第一个数为基准值。但若选取到的总是序列内的最值，快速排序时间复杂度会退化为平方阶。因此可考虑一些优化的选取方法：

• 三数取中：取序列首尾、中间的三个数，选取中间值
• 随机化：引入随机数，随机选择基准值下标

2.数列调整过程

选好基准值后，在待排序序列中设置两个哨兵，即首尾下标。若要排序为升序，右侧哨兵向左找一个比基准值小的数，左侧哨兵再向右找一个比基准值大的数，两数交换，直至碰面，碰面位置与基准值位置再交换即可。

以数列6 1 2 7 9 3 4 5 10 8为例：

说明\数组下标	0	1	2	3	4	5	6	7	8	9
选中基准6	6	1	2	7	9	3	4	5	10	8
r=9,往左找比6小的,找到r=7	6							5
l=0,往右找比6大的,找到l=3				7				5
l r做交换				5				7
r=7,往左找比6小的,找到r=6				5			4	7
l=3,往右找比6大的,找到l=4					9		4
l r做交换					4		9
r=6,往左找比6小的,找到r=5
l=4,往右找比6大的,发现l=r=5					4	3	9
l=r=5与基准交换	3					6

上表完成了当前数列的改动，接下来递归基准值左右两侧的序列，执行同样的操作。

全过程图示：

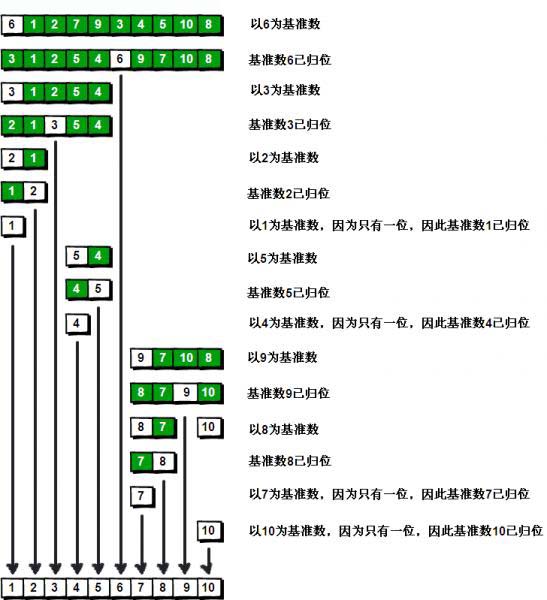
注意：查找时，右侧哨兵先动。

例题：

题目
CCFPB06D12 排序

#include<iostream>
using namespace std;

const int N = 1e5 + 5;
int a[N];
int n;

void show()
{
  for(int i = 1; i <= n; i++)
    cout << a[i] << ' ';
}

void quickSort(int l, int r)
{
  if(l >= r)
    return;
  int t = a[l];	//	基准值
  int i = l, j = r;	//	哨兵
  while(i < j){
    while(a[j] > t)
      j--;
    while(a[i] <= t && i < j)
      i++;
    if(i != j)
      swap(a[i], a[j]);
  }
  swap(a[l], a[i]);
  
  quickSort(l, i - 1);
  quickSort(i + 1, r);
}

int main()
{
  cin >> n;
  for(int i = 1; i <= n; i++)
    cin >> a[i];
  quickSort(1, n);
  show();
  
  return 0;
}

练习：

题目
CCFPB06D13合影效果
CCFPB06D14序列第K小
P4083 最长的美好子字符串