基础算法(base algorithm)简介

1、算法

算法（Algorithm）是指某类问题的解决方案，由一系列有限的指令所组成。也就是说，算法是解某一类特定问题的一组有限指令的集合。（就是解决问题的方法与步骤）

例如：如何把大象装入冰箱？

第一步：打开冰箱门

第二步：把大象放进去

第三步：关上冰箱门

例如：交换两个数。

首先用一个临时数值存储第一个数值。

把第一个数的值设置为第二个数的值。

把第二个数的值设置为临时的数值。

2、描述算法

算法可以用文字来描述，也可以用流程图、或者图示、表格、甚至伪代码来描述，这些都是与具体的 $\color{blue}代码实现无关$ 的。

例如－数组最大值算法

文字表示：

将一个max变量的值设置为第一个元素从第二个元素开始遍历数组，依次与max比较如果元素比max大，将max设置成该元素遍历结束之后，变量max的值就是最大值。

流程图表示：

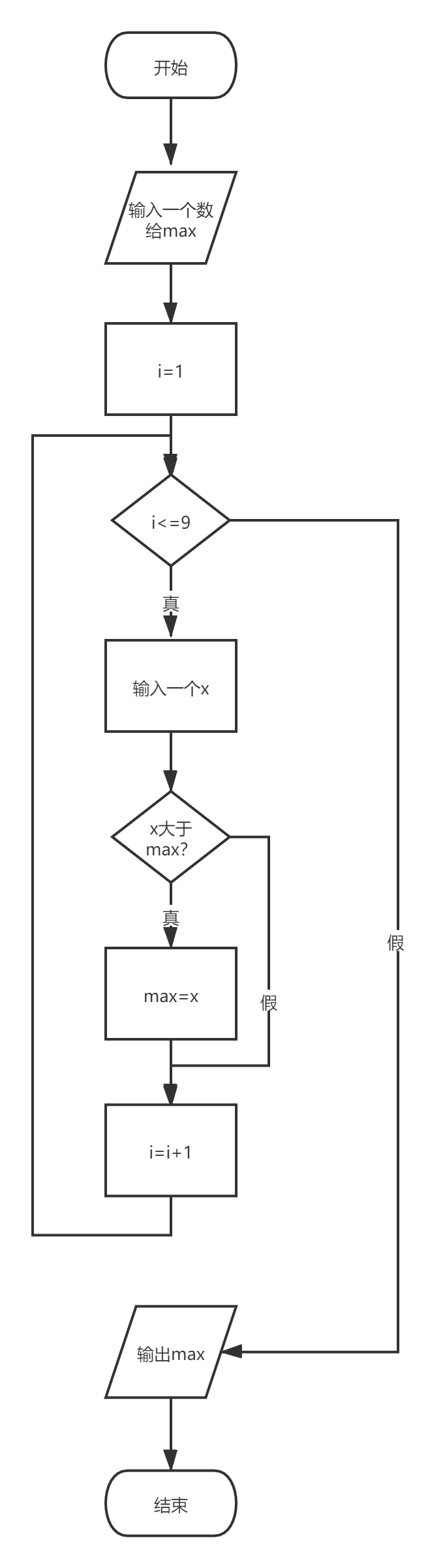
伪代码表示：

开始
    假设数组名为 array，其长度为 n
    设 max_value 为 array 的第一个元素，即 max_value = array[0]

    对于 i 从 1 到 n-1 执行以下步骤
        如果 array[i] > max_value
            则 max_value = array[i]

    输出 max_value
结束

3、算法的实现

算法可以用不同的语言代码实现，同一个算法即可以用c++实现，也可以用java、python实现。

例如c++实现：

int a=10, b=20;
int tmp = a;
a = b;
b = tmp;
cout << a << " " << b;

4、算法的特征（特性）

算法具有五个特征：

输入：有零个或多个输入。
输出：产生一个或多个输出。
有限性：算法中指令的执行次数和执行时间都是有限的。
确定性：每条指令均是清晰无歧义的，也即相同的输入只能得到相同的输出。
可行性：算法的操作都可以通过已经实现的基本运算执行有限次来实现。

注意：算法不等于程序，程序是可以无限的，例如死循环的程序。

5、算法与竞赛题

竞赛题往往把某种算法（或算法组合）包装成一个试题，赋予一定的故事背景，并根据算法的性能设定一定的数据范围。

在理解竞赛题的时候，要能透过题目的描述，看到背后的模型，找到适合此模型的算法。

6、练习题

交换算法

int a=10, b=20;
  int tmp = a;
  a = b;
  b = tmp;
  
  cout << a << " " << b;

CCFPB01D04 交换两数

最大值（最小值）算法要求：用文字描述写出求数组最大值的算法，放到多行注释里面。然后编写代码实现并测试，数据：{7, 8, 5, 3, 10}。

示例一：

/*
1. 变量max赋值为第一个元素
2. 从第二个元素开始遍历，如果元素大于max，就把max赋值为当前元素
3. 循环结束，输出max的值
*/
#include <iostream>
using namespace std;

int main() {
  int a[5] = {7, 8, 5, 3, 10};
  int max = a[0];
  for(int i=1; i<5; i++)
    if(a[i] > max)
      max = a[i];
 
  cout << max;
  return 0;
}

示例二：

#include <iostream>
using namespace std;

int main() {
  int a[5] = {7, 8, 5, 3, 10};
  int max = -0x3f3f3f3f;
  for(int i=0; i<5; i++)
    if(a[i] > max)
      max = a[i];
 
  cout << max;
  return 0;
}

正确答案：10

示例三：（最小值）

#include <iostream>
using namespace std;

int main() {
  int a[5] = {7, 8, 5, 3, 10};
  int minx = 0x3f3f3f3f;
  for(int i=0; i<5; i++)
    if(a[i] < minx)
      minx = a[i];
 
  cout << minx;
  return 0;
}

练习： YBTJ1112 最大值和最小值的差

数组平均值算法在注释里用文字描述求数组平均值的算法。写代码实现此算法，并测试，数据：{7, 8, 5, 3, 10}。

示例代码：

#include <iostream>
using namespace std;

long long sum; //注意变量类型为long long，
int temp;
int cnt;
double ave; //注意变量类型

int main()
{
  int a[5] = {7, 8, 5, 3, 10};
  for(int i = 0; i < 5; ++i)
  {
    cnt++;
    sum+=a[i];
  }
  ave = sum * 1.0 / cnt; // 注意，为什么要 * 1.0，整形 / 整形 = 整型变量
  cout << ave;
}

练习：YBTJ1061 求整数的和与均值